第66页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
1 (2025·南通海门区期末)如图,在$Rt△ABC$中,$∠C$$=90^{\circ },BC= 4,CA= 3$,则$△ABC$的内切圆半径为
1
.
答案:
1
2 教材P69思考与探索·拓展 尺规作图.(要求:用尺
规作图,保留作图痕迹,不写作法,不要求证明)
(1)如图(1),已知$△ABC$.求作:$△ABC$的内
切圆$\odot I;$
(2)如图(2),点C、D分别在$∠AOB$的两边上,用
直尺和圆规作一个圆,和OA、OB、CD都相切.
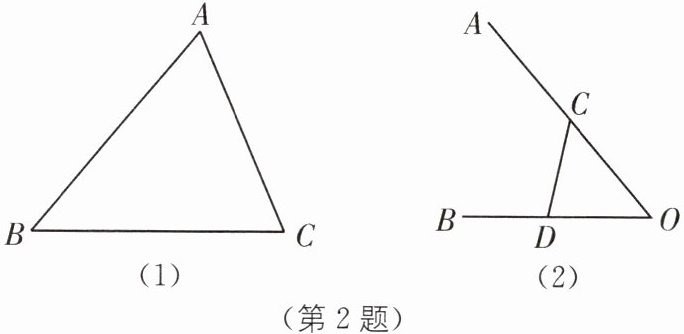
规作图,保留作图痕迹,不写作法,不要求证明)
(1)如图(1),已知$△ABC$.求作:$△ABC$的内
切圆$\odot I;$
(2)如图(2),点C、D分别在$∠AOB$的两边上,用
直尺和圆规作一个圆,和OA、OB、CD都相切.

答案:
(1)如图,作△ABC两个角的平分线交于点I,作IE⊥BC于点E,以点I为圆心,IE为半径作⊙I.
(2)有两种情况:①作∠ACD、∠BDC、∠AOB三个角中任意两个角的平分线交于点I,作IE⊥CD于点E,以点I为圆心,IE为半径作⊙I.②作∠OCD、∠CDO、∠AOB三个角中任意两个角的平分线交于点I',作I'E'⊥CD于点E',以点I'为圆心,I'E'为半径作⊙I'.图略.
(1)如图,作△ABC两个角的平分线交于点I,作IE⊥BC于点E,以点I为圆心,IE为半径作⊙I.
(2)有两种情况:①作∠ACD、∠BDC、∠AOB三个角中任意两个角的平分线交于点I,作IE⊥CD于点E,以点I为圆心,IE为半径作⊙I.②作∠OCD、∠CDO、∠AOB三个角中任意两个角的平分线交于点I',作I'E'⊥CD于点E',以点I'为圆心,I'E'为半径作⊙I'.图略.
3 (2025·南通海门区期中)如图,点I为$△ABC$的内心,若$∠A为50^{\circ }$,则$∠BIC$的度数为(

A.$105^{\circ }$
B.$100^{\circ }$
C.$115^{\circ }$
D.$130^{\circ }$
C
).
A.$105^{\circ }$
B.$100^{\circ }$
C.$115^{\circ }$
D.$130^{\circ }$
答案:
C
4 教材P69例4·改编 如图,$\odot I是△ABC$的内切圆,D、E、F为三个切点.若$∠DEF= 52^{\circ }$,则$∠A$的度数为(
A.$76^{\circ }$
B.$68^{\circ }$
C.$52^{\circ }$
D.$38^{\circ }$
A
).A.$76^{\circ }$
B.$68^{\circ }$
C.$52^{\circ }$
D.$38^{\circ }$
答案:
A
5 传统文化 《九章算术》 《九章算术》是我国古代数学名著,也是古代东方数学的代表作之一.书中记载了一个问题:“今有勾五步,股十二步,问勾中容圆径几何?”译文:“如图,今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的圆(内切圆)的直径是多少步?”根据题意,该直角三角形内切圆的直径为
4
步.
答案:
4
6 如图,已知在锐角三角形ABC中,$AC= BC.$
(1)请在图(1)中用无刻度的直尺和圆规作
$△ABC的内切圆\odot O$;(不写作法,保留作图
痕迹)
(2)在(1)的条件下,若$AC= 3,AB= 4$,求
$△ABC$内切圆的半径.(如需画草图,请使用
图(2))
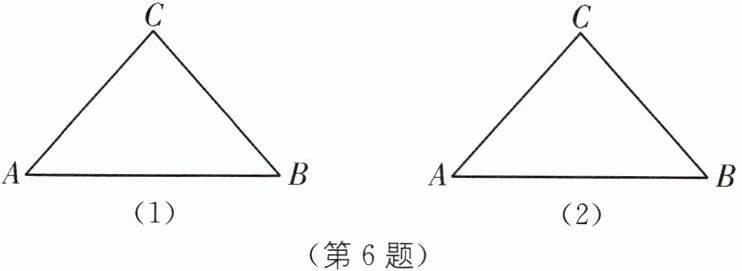
(1)请在图(1)中用无刻度的直尺和圆规作
$△ABC的内切圆\odot O$;(不写作法,保留作图
痕迹)
(2)在(1)的条件下,若$AC= 3,AB= 4$,求
$△ABC$内切圆的半径.(如需画草图,请使用
图(2))

答案:
(1)如图
(1),⊙O即为所求.
(2)如图
(2),连接OC,过点O分别作AB、AC、BC的垂线,垂足分别为D、E、F,⊙O的半径为r.
∵⊙O为△ABC的内切圆,
∴OD=OE=OF=r,CO平分∠ACB.
∵AC=BC,
∴CO⊥AB,
∴点C、O、D共线,
∴AD=BD=$\frac{1}{2}$AB=2. 在Rt△ACD中,CD=$\sqrt{3^2-2^2}$=$\sqrt{5}$.
∵S△AOB+S△AOC+S△BOC=S△ABC,
∴$\frac{1}{2}$×4×r+$\frac{1}{2}$×3×r+$\frac{1}{2}$×3×r=$\frac{1}{2}$×4×$\sqrt{5}$,解得r=$\frac{2\sqrt{5}}{5}$.故△ABC内切圆的半径为$\frac{2\sqrt{5}}{5}$.
(1)如图
(1),⊙O即为所求.
(2)如图
(2),连接OC,过点O分别作AB、AC、BC的垂线,垂足分别为D、E、F,⊙O的半径为r.
∵⊙O为△ABC的内切圆,
∴OD=OE=OF=r,CO平分∠ACB.
∵AC=BC,
∴CO⊥AB,
∴点C、O、D共线,
∴AD=BD=$\frac{1}{2}$AB=2. 在Rt△ACD中,CD=$\sqrt{3^2-2^2}$=$\sqrt{5}$.
∵S△AOB+S△AOC+S△BOC=S△ABC,
∴$\frac{1}{2}$×4×r+$\frac{1}{2}$×3×r+$\frac{1}{2}$×3×r=$\frac{1}{2}$×4×$\sqrt{5}$,解得r=$\frac{2\sqrt{5}}{5}$.故△ABC内切圆的半径为$\frac{2\sqrt{5}}{5}$.
查看更多完整答案,请扫码查看


