《2025年课时训练九年级数学上册苏科版江苏人民出版社》

10 新情境 数学与生活融合 某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面。
(1)若这个输水管道有水部分的水面宽$AB= 16cm$,水面最深地方的高度为4cm,求这个圆形截面的半径。
(2)在(1)的条件下,小明把一只宽12cm的方形小木船放在修好后的圆柱形水管里,已知船高出水面13cm,问此小船能顺利通过这个管道吗？

答案：

(1)如图
(1),O为圆心,过点O作OE⊥AB于点D,交弧AB于点E，连接OB.
　　　　　　　　
∵OE⊥AB,
∴BD=$\frac{1}{2}$AB=$\frac{1}{2}$×16 = 8(cm).
　由题意可知,ED = 4 cm.
　设半径为x cm,则OD=(x - 4)cm,
　在Rt△BOD中,由勾股定理,得$OD^{2}+BD^{2}=OB^{2}$,
∴$(x - 4)^{2}+8^{2}=x^{2}$,解得x = 10.
　即这个圆形截面的半径为10 cm.
(2)小船能顺利通过这个管道.理由如下:
　　　　　　　　
　如图
(2),由题意,得MN = 12 cm,连接OM，作EF⊥MN.
∴OM = 10 cm,MF=$\frac{1}{2}$MN = 6 cm,
∴在Rt△MOF中,OF=$\sqrt{OM^{2}-MF^{2}}$ = 8 cm,
∴DF = OF + OD = 8 + 6 = 14(cm).
∵14 cm＞13 cm,
∴小船能顺利通过这个管道.

11 中考新考法 方案设计 综合与实践
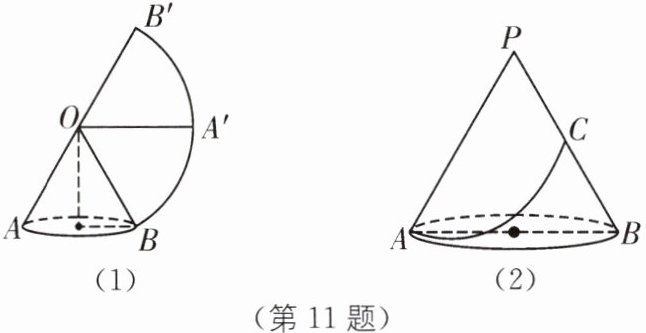
问题情境：如图(1),将一个圆锥的侧面展开后可得到一个圆心角为$n^{\circ}$,半径为l的扇形$BOB'$,圆锥底面是一个半径为r的圆。母线OA在展开图上对应的半径$OA'经过\overset{\frown}{BB'}$的中点。
特例研究：(1)当$r= 3$,$l= 9$时,$n= $______,展开图上,$OA'$与OB的夹角为______$^{\circ}$；
问题提出：(2)求证：$n= \frac{360r}{l}$；
问题解决：(3)如图(2),一种纸质圆锥形生日帽,底面直径为12cm,母线长也为12cm,为了美观,想在底面圆上一点A和与之相对的母线PB中点C之间拉一条细彩带进行装饰,求彩带长度的最小值。(提示：尝试画出圆锥侧面展开图)

答案：

(1)120　60　[解析]由题意,得扇形OBB'的弧长等于圆锥底面圆的周长，即$\frac{n\pi l}{180}=2\pi r$,即$n=\frac{360r}{l}$.
　当r = 3,l = 9时,$n=\frac{360×3}{9}=120$.
∵母线OA在展开图上对应的半径OA'经过$\overset{\frown}{BB'}$ 的中点,
∴OA'与OB的夹角为$\frac{1}{2}$×120° = 60°.
(2)由题意，得扇形OBB'的弧长等于圆锥底面圆的周长，即$\frac{n\pi l}{180}=2\pi r$,
∴$n=\frac{360r}{l}$.
(3)底面直径为12 cm,则半径r =6,而l = 12 = PA = PB,由
(2)得$n=\frac{360r}{l}=\frac{360×6}{12}=180$.
　由
(1)知,展开后∠APB=$\frac{1}{2}$n° = 90°,则∠P = 90°.
　如图所示，
∵C是PB的中点,
∴PC=$\frac{1}{2}$PB = 6.
　　　　　　　　　　　　　　　　
∵两点之间线段最短，
∴彩带长度
　的最小值为AC=$\sqrt{PA^{2}+PC^{2}}=\sqrt{12^{2}+6^{2}}=6\sqrt{5}$