《2025年课时训练九年级数学上册苏科版江苏人民出版社》

9 我们知道：过圆外一点所画的圆的两条切线长相等.
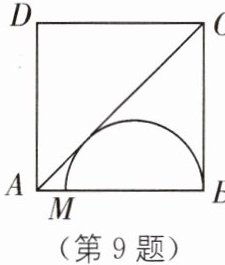
[问题解决]如图,现有一块边长为20m的正方形空地ABCD,在边AB取一点M,以MB长为直径,在这个正方形的空地内建一个半圆形儿童游乐场,过点C划出一条与这个半圆相切的分割线,正方形ABCD位于分割线右下方的部分作为娱乐区,娱乐区的最大面积等于(C).

$A.180m^2$
B.110$\sqrt{3}$m^2
$C.250m^2$
D.200$\sqrt{2}$m^2

答案： C　[解析]如图，当半圆面积最大,即点M与点A重合时，娱乐区的面积最大，设PC与半圆相切于点H,交AD于点P.
∵四边形ABCD是正方形,
∴PA⊥AB,CB⊥AB,
∴PA、CB分别是半圆的切线，
∴CH=CB=20m,PA=PH.设PA=xm,则PH=xm,PD=(20−x)m,PC=(x+20)m.在Rt△PDC中,PC²=PD²+DC²,
∴(x+20)²=(20−x)²+20²,
∴x=5,
∴PA=5m,
∴娱乐区的最大面积=梯形ABCP的面积=$\frac{1}{2}$(AP+BC)·AB=$\frac{1}{2}$×(5+20)×20=250(m²).故选C.

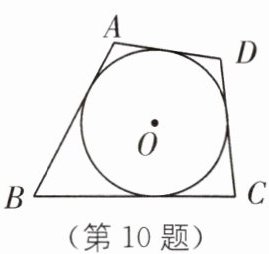
10 如图,四边形ABCD的各边都与圆相切,它的周长为18,若AB= 5,则CD的长为4.

答案： 4　[解析]如图,设四边形各边分别切⊙O于点E、F、G、H,根据切线长定理,得AE=AH,BE=BF,CF=CG,DG=DH,
∴AE+BE+DG+CG=AH+BF+DH+CF,
∴AB+CD=AD+BC,
∴AB+CD=$\frac{1}{2}$(AB+CD+AD+BC)=$\frac{1}{2}$×18=9,
∴CD=9−AB=4.知识拓展　由本题可以得出结论，圆的外切四边形，两组对边之和相等.

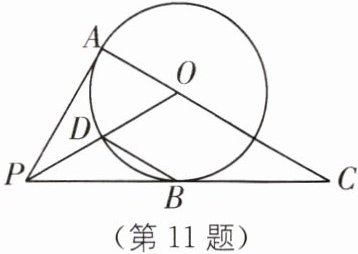
11 如图,PA、PB是$\odot O$的切线,A、B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交$\odot O$于点D.
(1)求证：PO平分∠APC；
(2)连接DB,若∠C= 30°,求证：DB//AC.

答案：
(1)如图，连接OB,
∵PA、PB是⊙O的切线，
∴OA⊥PA,OB⊥PB.又OA=OB,
∴PO平分∠APC.
(2)
∵OA⊥AP,OB⊥BP,
∴∠CAP=∠OBP=90°.
∵∠C=30°,
∴∠APC=90°−∠C=60°.
∵PO平分∠APC,
∴∠OPC=$\frac{1}{2}$∠APC=$\frac{1}{2}$×60°=30°,
∴∠POB=90°−∠OPC=90°−30°=60°.又OD=OB,
∴△ODB是等边三角形,
∴∠OBD=60°,
∴∠DBP=∠OBP−∠OBD=90°−60°=30°,
∴∠DBP=∠C,
∴DB//AC.

(1)当α= 90°时,b= 6,a= 8时,m=2,n=12.
(2)如图(1),α= 90°,则m=$\frac{ab}{a+b+c}$,n=$\frac{a+b+c}{2}$(用含有a、b、c的代数式表示)；并求出$\triangle ABC$的面积.(用含有m、n的代数式表示)
$mn$
(3)如图(2),α= 60°,求出$\triangle ABC$的面积.(用含有m、n的代数式表示)
$\sqrt{3}mn$

答案：
(1)2　12　[解析]
∵∠C=90°,b=6,a=8,
∴c=10.如图
(1),设点D、E、F分别是CA的延长线、CB的延长线、直线AB与⊙P的切点,连接PD、PE、PF、OA、OB、OC.
∵S△BCA=S△ABO+S△ACO+S△BCO,
∴$\frac{1}{2}$×6×8=$\frac{1}{2}$×10m+$\frac{1}{2}$×6m+$\frac{1}{2}$×8m,
∴m=2.由已知,得四边形DPEC为正方形,
∴n=PD=$\frac{1}{2}$(CD+CE).由切线长定理可知,AF=AD,BF=BE,
∴n=$\frac{1}{2}$(CD+CE)=$\frac{1}{2}$(AD+AC+BE+BC)=$\frac{1}{2}$(AB +AC+BC)=$\frac{1}{2}$×(10+6+8)=12.
(2)$\frac{ab}{a+b+c}$　$\frac{a+b+c}{2}$　[解析]如图
(1),由切线的性质可知,PD⊥CD,PE⊥BC,PF⊥AB,
∴PD=PE=PF.设△ABC的面积为S△ABC,周长为C△ABC,同
(1),根据面积法可知m=$\frac{2S_{\triangle ABC}}{C_{\triangle ABC}}$=$\frac{2×\frac{1}{2}ab}{a+b+c}$=$\frac{ab}{a+b+c}$.
∵n=$\frac{1}{2}$(CD+CE)=$\frac{1}{2}$(AD+AC+BE+BC)=$\frac{1}{2}$(AB +AC+BC)=$\frac{1}{2}$C△ABC=$\frac{a+b+c}{2}$,
∴S△ABC=$\frac{mC_{\triangle ABC}}{2}$=mn.
(3)如图
(2),连接CP,设点D、E分别是CA的延长线、CB的延长线与⊙P的切点,连接PD、PE，由切线长定理，得CD=CE=$\frac{1}{2}$(CD+CE)=$\frac{1}{2}$(AD+AC+BE+BC)=$\frac{1}{2}$(AB+AC+BC)=$\frac{1}{2}$C△ABC.
∵PD⊥CD,PE⊥BC,且PD=PE,
∴CP平分∠ACB,
∴∠PCE=30°,
∴PC=2PE,
∴CE=$\sqrt{PC^{2}-PE^{2}}$=$\sqrt{3}$PE.
∴n=PE=$\frac{CE}{\sqrt{3}}$=$\frac{C_{\triangle ABC}}{2\sqrt{3}}$=$\frac{\sqrt{3}C_{\triangle ABC}}{6}$,
∵m=$\frac{2S_{\triangle ABC}}{C_{\triangle ABC}}$，
∴S△ABC=$\frac{mC_{\triangle ABC}}{2}$=$\sqrt{3}$mn.