第78页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
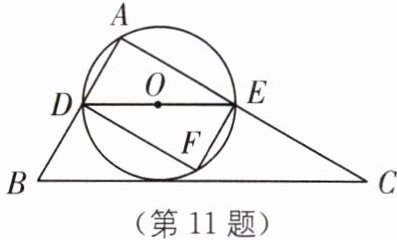
11 如图,在$\triangle ABC$中,$∠A= 90^{\circ },∠B= 60^{\circ },AB= 3$,点$D从点A$以每秒1个单位长度的速度向点$B$运动(点$D不与点B$重合),过点$D作DE// BC交AC于点E$,以$DE为直径作\odot O$,并在$\odot O内作内接矩形ADFE$,设点$D的运动时间为t$秒.
(1)用含$t的代数式表示\triangle DEF的面积S$.
(2)当$t$为何值时,$\odot O与直线BC$相切?
(1)用含$t的代数式表示\triangle DEF的面积S$.
(2)当$t$为何值时,$\odot O与直线BC$相切?

答案:
(1)
∵DE//BC,
∴∠ADE=∠B=60°.在△ADE中,∠A=90°,AD=t,DE=2AD=2t,
∴AE=$\sqrt{DE^2-AD^2}$=$\sqrt{3}$t.又四边形ADFE是矩形,
∴S△DEF=S△ADE=$\frac{1}{2}$AD·AE=$\frac{1}{2}$t×$\sqrt{3}$t=$\frac{\sqrt{3}}{2}$t²(0<t<3),
∴S=$\frac{\sqrt{3}}{2}$t²(0<t<3).
(2)如图,过点O作OG⊥BC于点G,过点D作DH⊥BC于点H.

∵DE//BC,
∴OG=DH,∠DHB=90°.在Rt△DBH中,∠B=60°,BD=AB−AD=3−t,
∴BH=$\frac{1}{2}$BD,
∴DH=$\sqrt{BD^2-BH^2}$=$\frac{\sqrt{3}}{2}$BD=$\frac{\sqrt{3}}{2}$(3−t),
∴OG=$\frac{\sqrt{3}}{2}$(3−t).当OG=$\frac{1}{2}$DE时,⊙O与BC相切.
∵在△ADE中,∠A=90°,∠ADE=60°,AD=t,
∴DE=2AD=2t,
∴$\frac{\sqrt{3}}{2}$(3−t)=$\frac{1}{2}$×2t,
∴t=6$\sqrt{3}$−9.故当t=6$\sqrt{3}$−9时,⊙O与直线BC相切.
(1)
∵DE//BC,
∴∠ADE=∠B=60°.在△ADE中,∠A=90°,AD=t,DE=2AD=2t,
∴AE=$\sqrt{DE^2-AD^2}$=$\sqrt{3}$t.又四边形ADFE是矩形,
∴S△DEF=S△ADE=$\frac{1}{2}$AD·AE=$\frac{1}{2}$t×$\sqrt{3}$t=$\frac{\sqrt{3}}{2}$t²(0<t<3),
∴S=$\frac{\sqrt{3}}{2}$t²(0<t<3).
(2)如图,过点O作OG⊥BC于点G,过点D作DH⊥BC于点H.

∵DE//BC,
∴OG=DH,∠DHB=90°.在Rt△DBH中,∠B=60°,BD=AB−AD=3−t,
∴BH=$\frac{1}{2}$BD,
∴DH=$\sqrt{BD^2-BH^2}$=$\frac{\sqrt{3}}{2}$BD=$\frac{\sqrt{3}}{2}$(3−t),
∴OG=$\frac{\sqrt{3}}{2}$(3−t).当OG=$\frac{1}{2}$DE时,⊙O与BC相切.
∵在△ADE中,∠A=90°,∠ADE=60°,AD=t,
∴DE=2AD=2t,
∴$\frac{\sqrt{3}}{2}$(3−t)=$\frac{1}{2}$×2t,
∴t=6$\sqrt{3}$−9.故当t=6$\sqrt{3}$−9时,⊙O与直线BC相切.
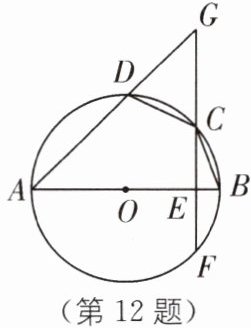
12 原创素养题 模型观念 如图,四边形$ABCD内接于\odot O$,$AB是\odot O$的直径,过点$C作CE⊥AB于点E$,交$\odot O于点F$,交$AD的延长线于点G$.
(1)连接$DF$,求证$∠CDG= ∠ADF$;
(2)过点$C作CH⊥AG于点H$,若$CH= CE$,求证:$CH为\odot O$的切线.
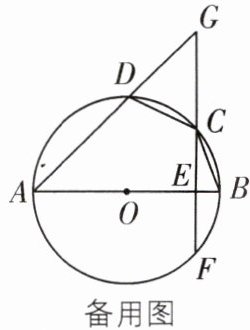
(1)连接$DF$,求证$∠CDG= ∠ADF$;
(2)过点$C作CH⊥AG于点H$,若$CH= CE$,求证:$CH为\odot O$的切线.


答案:
(1)如图
(1),连接DF.
∵CE⊥直径AB,
∴$\overset{\frown}{AC}$=$\overset{\frown}{AF}$,
∴∠ADF=∠ABC.
∵∠ADC+∠ABC=180°,∠ADC+∠CDG=180°,
∴∠CDG=∠ABC,
∴∠CDG=∠ADF.

(2)如图
(2),作CH⊥AG于点H,连接AC、OC.
∵CH=CE,CH⊥AG,CE⊥AB,
∴AC平分∠GAB,
∴∠DAC=∠OAC.
∵OA=OC,
∴∠OAC=∠OCA,
∴∠OCA=∠DAC,
∴AD//OC.
∵CH⊥AD,
∴OC⊥CH.
∵OC为⊙O的半径,
∴CH为⊙O的切线.
(1)如图
(1),连接DF.
∵CE⊥直径AB,
∴$\overset{\frown}{AC}$=$\overset{\frown}{AF}$,
∴∠ADF=∠ABC.
∵∠ADC+∠ABC=180°,∠ADC+∠CDG=180°,
∴∠CDG=∠ABC,
∴∠CDG=∠ADF.

(2)如图
(2),作CH⊥AG于点H,连接AC、OC.
∵CH=CE,CH⊥AG,CE⊥AB,
∴AC平分∠GAB,
∴∠DAC=∠OAC.
∵OA=OC,
∴∠OAC=∠OCA,
∴∠OCA=∠DAC,
∴AD//OC.
∵CH⊥AD,
∴OC⊥CH.
∵OC为⊙O的半径,
∴CH为⊙O的切线.
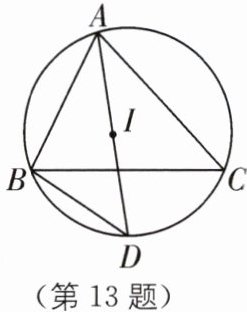
13 (2025·河南三门峡灵宝期中)如图,$I是\triangle ABC$的内心,$AI的延长线交\triangle ABC的外接圆于点D$.
(1)求证:$∠BAD= ∠CBD$;
(2)求证:$BD= ID$;
(3)连接$BI$、$CI$,求证:点$D是\triangle BIC$的外心.
(1)求证:$∠BAD= ∠CBD$;
(2)求证:$BD= ID$;
(3)连接$BI$、$CI$,求证:点$D是\triangle BIC$的外心.

答案:
(1)
∵点I是△ABC的内心,
∴∠BAD=∠CAD.
∵∠CBD=∠CAD,
∴∠BAD=∠CBD.
(2)如图
(1),连接BI,

∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI.
∵∠CBD=∠CAD,
∴∠BAD=∠CBD=∠CAD,
∴∠BID=∠ABI+∠BAD.
∵∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴ID=BD.
(3)如图
(2),连接BI、CI、DC,

∵∠BAD=∠CAD,
∴$\overset{\frown}{BD}$=$\overset{\frown}{CD}$,
∴BD=CD,
∴BD=CD=ID,
∴点D是△BIC的外心.
(1)
∵点I是△ABC的内心,
∴∠BAD=∠CAD.
∵∠CBD=∠CAD,
∴∠BAD=∠CBD.
(2)如图
(1),连接BI,

∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI.
∵∠CBD=∠CAD,
∴∠BAD=∠CBD=∠CAD,
∴∠BID=∠ABI+∠BAD.
∵∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴ID=BD.
(3)如图
(2),连接BI、CI、DC,

∵∠BAD=∠CAD,
∴$\overset{\frown}{BD}$=$\overset{\frown}{CD}$,
∴BD=CD,
∴BD=CD=ID,
∴点D是△BIC的外心.
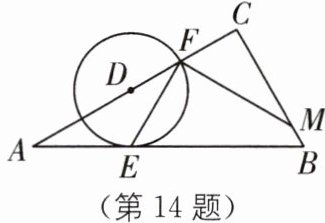
14 一题多问 如图,$∠C= 90^{\circ },∠A= 30^{\circ },AB= 6$,射线$AC上有一个动点D$,以$D$为圆心,作$\odot D与AB$相切,切点为$E$,$\odot D与射线AC交于F$,连接$EF$,作$MF⊥EF$,交直线$BC于点M$,设半径为$r$.
(1)证明:$AE= EF$;
(2)当$\odot D与BC$相切时,求$r$;
(3)当$M在\odot D$内时,求$r$的取值范围.
(1)证明:$AE= EF$;
(2)当$\odot D与BC$相切时,求$r$;
(3)当$M在\odot D$内时,求$r$的取值范围.

答案:
(1)如图
(1),连接DE.
∵⊙D与AB相切于点E,
∴∠AED=90°.
∵∠A=30°,
∴∠ADE=60°.
∵DE=DF,
∴∠DEF=∠DFE.
∵∠DEF+∠DFE=∠ADE,
∴∠DEF=∠DFE=30°,
∴∠A=∠DFE,
∴AE=EF.

(2)
∵∠C=90°,∠A=30°,AB=6,
∴BC=3,AC=3$\sqrt{3}$.①D在线段AC上,
∵AD=2r,CD=r,
∴2r+r=3$\sqrt{3}$,
∴r=$\sqrt{3}$.②D在线段AC的延长线上.
∵AD=2r,CD=r,
∴2r−r=3$\sqrt{3}$,
∴r=3$\sqrt{3}$.综上,r=$\sqrt{3}$或3$\sqrt{3}$.
(3)找临界位置:①D在线段AC上,⊙D与BC相切,此时r=$\sqrt{3}$.②如图
(2),M在⊙D上,连接EM.
∵∠MFE=90°,
∴EM为直径,
∴EM过点D.
∵∠MDF=∠ADE=60°,DM=DF,
∴△MDF为等边三角形.又MC⊥DF,
∴DF=2DC,AD=2r,CD=3$\sqrt{3}$−2r,DF=r,
∴r=2(3$\sqrt{3}$−2r),解得r=$\frac{6\sqrt{3}}{5}$.综上,r的取值范围为$\sqrt{3}$<r<$\frac{6\sqrt{3}}{5}$.
(1)如图
(1),连接DE.
∵⊙D与AB相切于点E,
∴∠AED=90°.
∵∠A=30°,
∴∠ADE=60°.
∵DE=DF,
∴∠DEF=∠DFE.
∵∠DEF+∠DFE=∠ADE,
∴∠DEF=∠DFE=30°,
∴∠A=∠DFE,
∴AE=EF.

(2)
∵∠C=90°,∠A=30°,AB=6,
∴BC=3,AC=3$\sqrt{3}$.①D在线段AC上,
∵AD=2r,CD=r,
∴2r+r=3$\sqrt{3}$,
∴r=$\sqrt{3}$.②D在线段AC的延长线上.
∵AD=2r,CD=r,
∴2r−r=3$\sqrt{3}$,
∴r=3$\sqrt{3}$.综上,r=$\sqrt{3}$或3$\sqrt{3}$.
(3)找临界位置:①D在线段AC上,⊙D与BC相切,此时r=$\sqrt{3}$.②如图
(2),M在⊙D上,连接EM.
∵∠MFE=90°,
∴EM为直径,
∴EM过点D.
∵∠MDF=∠ADE=60°,DM=DF,
∴△MDF为等边三角形.又MC⊥DF,
∴DF=2DC,AD=2r,CD=3$\sqrt{3}$−2r,DF=r,
∴r=2(3$\sqrt{3}$−2r),解得r=$\frac{6\sqrt{3}}{5}$.综上,r的取值范围为$\sqrt{3}$<r<$\frac{6\sqrt{3}}{5}$.
查看更多完整答案,请扫码查看


