第60页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
1 (2025·无锡新吴区期末)如图,四边形ABCD是$\odot O$的内接四边形,$∠AOC= 142^{\circ }$,则$∠ABC$的度数是(
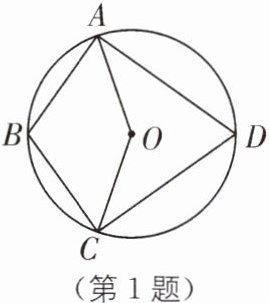
A.$109^{\circ }$
B.$142^{\circ }$
C.$45^{\circ }$
D.$19^{\circ }$
A
).
A.$109^{\circ }$
B.$142^{\circ }$
C.$45^{\circ }$
D.$19^{\circ }$
答案:
A
2 原创素养题 几何直观 如图,四边形ABCD内接于$\odot O$,F是$\widehat {CD}$上一点,且$\widehat {DF}= \widehat {BC}$,连接CF并延长交AD的延长线于点E,连接AC,若$∠ABC= 105^{\circ },∠BAC= 25^{\circ }$,则$∠E$的度数为(
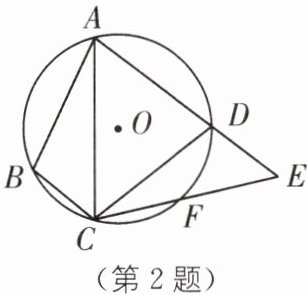
A.$60^{\circ }$
B.$55^{\circ }$
C.$50^{\circ }$
D.$45^{\circ }$
C
).
A.$60^{\circ }$
B.$55^{\circ }$
C.$50^{\circ }$
D.$45^{\circ }$
答案:
C
3 (2024·高邮期中)如图,小明为了测量圆形鼓面的直径,将直角三角板$30^{\circ }$角的顶点落在鼓面圆上任意一点P,三角板的两边分别交圆于点A、B,若测量得到弦AB的长为16cm,则鼓面圆的直径为(
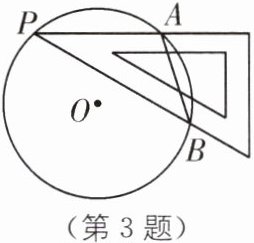
A.16cm
B.30cm
C.32cm
D.36cm
C
).
A.16cm
B.30cm
C.32cm
D.36cm
答案:
C
4 (2025·南京鼓楼区期末)如图,以AB为直径的半圆经过$\triangle ADE$的顶点D、E,点C在AB上,$AC= AD$,若$∠ADC= 80^{\circ }$,则$∠AED= $
110°
.
答案:
110°
5 已知点$A(1,0)$、点$B(5,0)$,点P是该平面直角坐标系内的一个动点.若点P在y轴的负半轴上,且$∠APB= 30^{\circ }$,则满足条件的点P的坐标为____.
答案:
(0,−2$\sqrt{3}$−$\sqrt{7}$)或(0,−2$\sqrt{3}$+$\sqrt{7}$) [解析]
∵∠APB = 30°,
∴点A、B、P在以点C为圆心,CA为半径的圆上,且∠ACB = 2∠APB = 60°,
∴△ABC为等边三角形,
∴CA = CB = AB = 4.
如图,⊙C交y轴于点P和P',连接CP,过点C作CD⊥AB于点D,CE⊥y轴于点E,则AD = DB = 2,PE = P'E.
∵AD = 2,CA = 4,
∴CD = 2$\sqrt{3}$,OD = OA + AD = 3,
∴EC = 3.在Rt△PCE中,PE = $\sqrt{4²−3²}$ = $\sqrt{7}$.
∵OE = CD = 2$\sqrt{3}$,
∴OP' = 2$\sqrt{3}$ - $\sqrt{7}$,OP = 2$\sqrt{3}$ + $\sqrt{7}$.
∴P(0,−2$\sqrt{3}$−$\sqrt{7}$),P'(0,−2$\sqrt{3}$+$\sqrt{7}$).
∴所有满足条件的点P的坐标为(0,−2$\sqrt{3}$−$\sqrt{7}$)或(0,−2$\sqrt{3}$+$\sqrt{7}$).

(0,−2$\sqrt{3}$−$\sqrt{7}$)或(0,−2$\sqrt{3}$+$\sqrt{7}$) [解析]
∵∠APB = 30°,
∴点A、B、P在以点C为圆心,CA为半径的圆上,且∠ACB = 2∠APB = 60°,
∴△ABC为等边三角形,
∴CA = CB = AB = 4.
如图,⊙C交y轴于点P和P',连接CP,过点C作CD⊥AB于点D,CE⊥y轴于点E,则AD = DB = 2,PE = P'E.
∵AD = 2,CA = 4,
∴CD = 2$\sqrt{3}$,OD = OA + AD = 3,
∴EC = 3.在Rt△PCE中,PE = $\sqrt{4²−3²}$ = $\sqrt{7}$.
∵OE = CD = 2$\sqrt{3}$,
∴OP' = 2$\sqrt{3}$ - $\sqrt{7}$,OP = 2$\sqrt{3}$ + $\sqrt{7}$.
∴P(0,−2$\sqrt{3}$−$\sqrt{7}$),P'(0,−2$\sqrt{3}$+$\sqrt{7}$).
∴所有满足条件的点P的坐标为(0,−2$\sqrt{3}$−$\sqrt{7}$)或(0,−2$\sqrt{3}$+$\sqrt{7}$).

6 如图(1),在$Rt\triangle ABC$中,$∠B= 90^{\circ },∠C= 40^{\circ }$,以AB为直径画$\odot O$交AC于点D,E是线段AB上的动点,延长DE交$\odot O$于点F,连接AF.
(1)如图(1),求$∠F$的度数;
(2)如图(2),当$AE= AD$时,求$∠DFO$的度数.
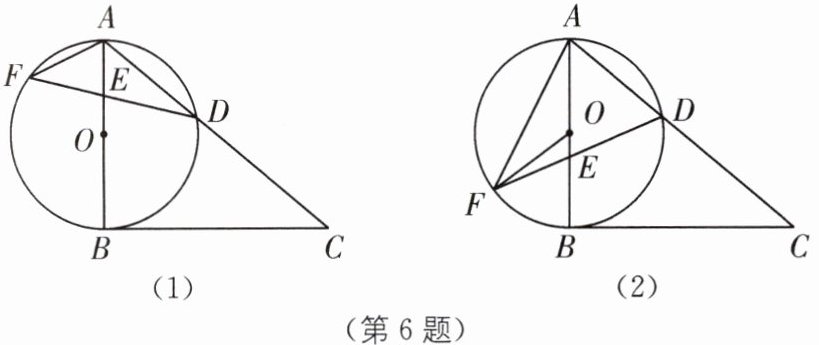
(1)如图(1),求$∠F$的度数;
(2)如图(2),当$AE= AD$时,求$∠DFO$的度数.

答案:
(1)连接OD.在Rt△ABC中,∠B = 90°,∠C = 40°,
∴∠BAC = 50°.
∵OA = OD,
∴∠ODA = ∠OAD = 50°,
∴∠AOD = 180°−50°−50° = 80°,
∴∠F = $\frac{1}{2}$∠AOD = 40°.
(2)连接OD.
在Rt△ABC中,∠B = 90°,∠C = 40°,
∴∠BAC = 50°.
∵OA = OD,
∴∠ODA = ∠OAD = 50°.
∵AE = AD,
∴∠ADE = ∠AED = $\frac{1}{2}$×(180°−50°) = 65°,
∴∠ODF = ∠ADE−∠ODA = 65°−50° = 15°.
∵OF = OD,
∴∠DFO = ∠ODF = 15°.
(1)连接OD.在Rt△ABC中,∠B = 90°,∠C = 40°,
∴∠BAC = 50°.
∵OA = OD,
∴∠ODA = ∠OAD = 50°,
∴∠AOD = 180°−50°−50° = 80°,
∴∠F = $\frac{1}{2}$∠AOD = 40°.
(2)连接OD.
在Rt△ABC中,∠B = 90°,∠C = 40°,
∴∠BAC = 50°.
∵OA = OD,
∴∠ODA = ∠OAD = 50°.
∵AE = AD,
∴∠ADE = ∠AED = $\frac{1}{2}$×(180°−50°) = 65°,
∴∠ODF = ∠ADE−∠ODA = 65°−50° = 15°.
∵OF = OD,
∴∠DFO = ∠ODF = 15°.
7 中考新考法 组合条件开放 如图,BC是$\odot O$的直径,点A、E在$\odot O$上,且在直径BC的两侧,点D在直径BC上,AD的延长线交BE于点F,AC、BE的延长线交于点G,给出下列信息:
①$AD⊥BC$;②$\widehat {AB}= \widehat {AE}$;③$AF= FG.$
请从上述三条信息中选择两条作为补充条件,余下的一条作为结论组成一个真命题,并说明理由.你选择的补充条件是
证明:
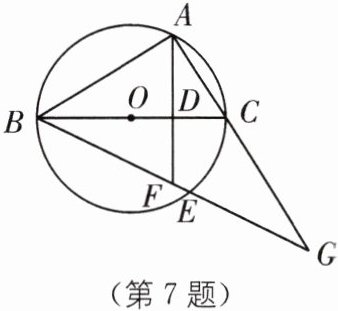
①$AD⊥BC$;②$\widehat {AB}= \widehat {AE}$;③$AF= FG.$
请从上述三条信息中选择两条作为补充条件,余下的一条作为结论组成一个真命题,并说明理由.你选择的补充条件是
①②
,结论是③
.(填写序号)证明:

∵BC为直径,AD⊥BC,
∴∠BAC = ∠ADC = 90°,
∴∠BAD + ∠CAD = 90°,∠ACB + ∠CAD = 90°.
∴∠BAD = ∠ACB.
∵$\widehat {AE}=\widehat {AB}$,
∴∠ABE = ∠ACB,
∴∠ABE = ∠BAD,
∵∠BAD + ∠CAD = 90°,∠ABE + ∠AGB = 90°,
∴∠DAC = ∠AGB,
∴FA = FG.
∴∠BAC = ∠ADC = 90°,
∴∠BAD + ∠CAD = 90°,∠ACB + ∠CAD = 90°.
∴∠BAD = ∠ACB.
∵$\widehat {AE}=\widehat {AB}$,
∴∠ABE = ∠ACB,
∴∠ABE = ∠BAD,
∵∠BAD + ∠CAD = 90°,∠ABE + ∠AGB = 90°,
∴∠DAC = ∠AGB,
∴FA = FG.
答案:
选择的补充条件是①②,结论是③或补充条件是①③,结论是②或补充条件是②③,结论是①.
补充条件是①②,结论是③.证明如下:
∵BC为直径,AD⊥BC,
∴∠BAC = ∠ADC = 90°,
∴∠BAD + ∠CAD = 90°,∠ACB + ∠CAD = 90°.
∴∠BAD = ∠ACB.
∵$\widehat {AE}=\widehat {AB}$,
∴∠ABE = ∠ACB,
∴∠ABE = ∠BAD,
∵∠BAD + ∠CAD = 90°,∠ABE + ∠AGB = 90°,
∴∠DAC = ∠AGB,
∴FA = FG.
补充条件是①②,结论是③.证明如下:
∵BC为直径,AD⊥BC,
∴∠BAC = ∠ADC = 90°,
∴∠BAD + ∠CAD = 90°,∠ACB + ∠CAD = 90°.
∴∠BAD = ∠ACB.
∵$\widehat {AE}=\widehat {AB}$,
∴∠ABE = ∠ACB,
∴∠ABE = ∠BAD,
∵∠BAD + ∠CAD = 90°,∠ABE + ∠AGB = 90°,
∴∠DAC = ∠AGB,
∴FA = FG.
查看更多完整答案,请扫码查看


