《2025年综合应用创新题典中点七年级数学下册冀教版》

15. [2024·烟台 情境题·科技创新]目前全球最薄的手撕钢产自中国，厚度只有 0.015 毫米，约是 A4 纸厚度的六分之一. 已知 1 毫米 = 1 百万纳米，0.015 毫米等于多少纳米？将结果用科学记数法表示为（ ）
A. $0.15\times10^{5}$ 纳米
B. $1.5\times10^{4}$ 纳米
C. $15\times10^{-5}$ 纳米
D. $1.5\times10^{-6}$ 纳米

答案： B

16. 用科学记数法表示的数 $-1.23\times10^{-4}$，化为原数是 \underline{\hspace{50pt}}.

答案： -0.000123

17. [2024乐山]已知 $a - b = 3$，$ab = 10$，则 $a^{2}+b^{2}=\underline{\hspace{50pt}}$.

答案： 29

18. 设 $M = 123456789\times123456786$，$N = 123456788\times123456787$，试比较 $M$ 与 $N$ 的大小.

答案： 【解】设a = 123456788，
则M=(a + 1)(a - 2)=a^2 - a - 2，N=a(a - 1)=a^2 - a.
∵M - N=-2＜0，
∴M＜N.

19. 已知 $a=\dfrac{3}{8}x - 20$，$b=\dfrac{3}{8}x - 18$，$c=\dfrac{3}{8}x - 16$，求 $a^{2}+b^{2}+c^{2}-ab - ac - bc$ 的值.

答案： 【解】原式=(a^{2} + b^2 + c^2 - ab - ac - bc)×2×$\frac{1}{2}$
=$\frac{1}{2}$(2a^2 + 2b^2 + 2c^2 - 2ab - 2ac - 2bc)
=$\frac{1}{2}$[(a^2 + b^2 - 2ab)+(a^2 + c^2 - 2ac)+(b^2 + c^2 - 2bc)]
=$\frac{1}{2}$[(a - b)^2+(a - c)^2+(b - c)^2].
将a=$\frac{3}{8}$x - 20，b=$\frac{3}{8}$x - 18，c=$\frac{3}{8}$x - 16代入，得
原式=$\frac{4 + 16 + 4}{2}$=12.

20. [2024石家庄校级月考]已知 $n$ 是正整数，若 $4^{n}+4^{n}+4^{n}+4^{n}=8^{4}$，则 $n$ 的值是（ ）
A. 4
B. 5
C. 6
D. 8

答案： B 【点拨】
∵4^n + 4^n + 4^n + 4^n = 4×4^n = 4^(n + 1)=(2^2)^(n + 1)=2^(2n + 2)，8^4=(2^3)^4 = 2^12，
∴2n + 2 = 12，解得n = 5.故选B.

21. [母题 教材 P108 复习题 T14]如果 $x^{2}+px - 6=(x + q)(x - 2)$，那么 $p=\underline{\hspace{50pt}}$，$q=\underline{\hspace{50pt}}$.

答案： 1；3 【点拨】
∵x^2 + px - 6=(x + q)(x - 2)=x^2+(q - 2)x - 2q，
∴p = q - 2，-2q = -6，解得p = 1，q = 3.

22. [新考法 数形结合法]把几个图形拼成一个新的图形，再通过两种不同的方法计算同一个图形的面积，可以得到一个等式，也可以求出一些图形的面积. 例如，由图①，可得等式：$(a + 2b)(a + b)=a^{2}+3ab + 2b^{2}$.
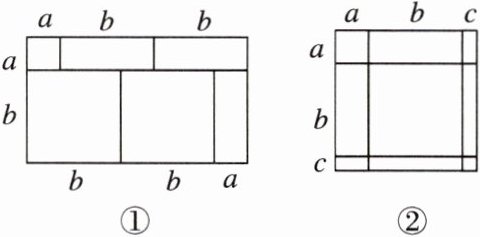
(1)如图②，将几个面积不等的小正方形与小长方形拼成一个边长为 $a + b + c$ 的正方形，试用不同的形式表示这个大正方形的面积，你能发现什么结论？请用等式表示出来.
(2)利用(1)中所得到的结论，解决下面的问题：已知 $a + b + c = 10$，$ab + bc + ac = 30$，求 $a^{2}+b^{2}+c^{2}$ 的值. 图①： 图②： （图①为两个长方形拼接图，长分别为 $a + 2b$ 和 $a + b$；图②为边长为 $a + b + c$ 的正方形分割图）

答案： 【解】
(1)(a + b + c)^2=a^2 + b^2 + c^2 + 2ab + 2bc + 2ac
(2)
∵a + b + c = 10，ab + bc + ac = 30，
∴a^2 + b^2 + c^2=(a + b + c)^2 - 2(ab + bc + ac)=100 - 60 = 40.