《2025年综合应用创新题典中点七年级数学下册冀教版》

1. [2024邢台期中] 若方程组$\begin{cases}x + 2y = 4\\......\end{cases}$是二元一次方程组，则“......”不可能是 （ ）

A. $x = -1$
B. $y + 2 = 0$
C. $xy = 0$
D. $x - y = -1$

答案： C

2. 下列说法中，不正确的是 （ ）
A. 方程$x = y$是二元一次方程
B. 任何一个二元一次方程都只有一组解
C. 方程$x - 2y = 5$有无数组解
D. $\begin{cases}x = 2\\y = -1\end{cases}$是方程$x - 2y = 4$的解

答案： B

3. [2024沧州期中] 下列是二元一次方程$3x - 2y = 0$的解的是 （ ）
A. $\begin{cases}x = 3\\y = 2\end{cases}$
B. $\begin{cases}x = 3\\y = -2\end{cases}$
C. $\begin{cases}x = -3\\y = -2\end{cases}$
D. $\begin{cases}x = 2\\y = 3\end{cases}$

答案： D

4. [真实情境题 航天科技] 为了庆祝2024年11月4日神舟十八号载人飞船在东风着陆场成功着陆，某学校组织学生开展有关航空航天的知识竞赛. 竞赛共有60道题，小荣同学答对了$x$道题，答错了$y$道题（不答视为答错），且答对题数比答错题数的7倍还多4道，那么下面列出的方程组中正确的是 （ ）
A. $\begin{cases}x + y = 60\\x - 7y = 4\end{cases}$
B. $\begin{cases}x + y = 60\\y - 7x = 4\end{cases}$
C. $\begin{cases}x = 60 - y\\x = 7y - 4\end{cases}$
D. $\begin{cases}y = 60 - x\\y = 7x - 4\end{cases}$

答案： A

5. [母题 教材P4练习T1] 将方程$2x + y = 5$写成用含$x$的代数式表示$y$的形式：__________.

答案： $y = 5 - 2x$

6. [2024北京大兴区期末] 已知方程$(m + 1)x - 3y^{|m|} = 0$是关于$x$，$y$的二元一次方程，则$m$的值为__________.

答案： 1

7. [新视角 结论开放题] 写出二元一次方程$2x + 3y = 8$的一组整数解：__________.

答案： $\begin{cases}x = 1\\y = 2\end{cases}$（答案不唯一）

8. [母题 教材P3一起探究] 已知方程组$\begin{cases}3x + y = -1\\2x - 3y = -8\end{cases}$
(1)$x$分别取$-3$，$-1$，$0$，$2$，填写下表：

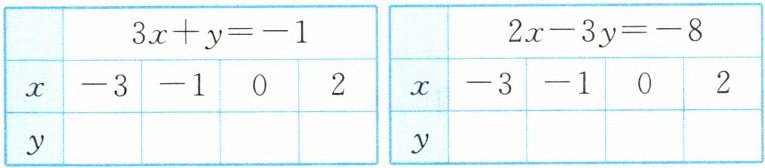
(2)根据(1)中的数据写出方程组的解.

答案： 【解】
(1)$8;2;-1;-7;\frac{2}{3};2;\frac{8}{3};4$
(2)方程组的解为$\begin{cases}x = -1\\y = 2\end{cases}$

9. 如果方程组$\begin{cases}x + y = ★\\2x + y = 16\end{cases}$的解为$\begin{cases}x = 6\\y = ■\end{cases}$，那么被“★，■”遮住的两个数分别为 （ ）
A. 3，10
B. 4，10
C. 10，4
D. 10，3

答案： C

10. [2024泰安] [新考向 数学文化] 我国古代《四元玉鉴》中记载“二果问价”问题，其内容大致如下：用九百九十九文钱，可买甜果苦果共一千个，若…，…，试问买甜果、苦果各几个？若设买甜果$x$个，买苦果$y$个，可列出符合题意的二元一次方程组$\begin{cases}x + y = 1000\\\frac{11}{9}x + \frac{4}{7}y = 999\end{cases}$，根据已有信息，题中用“…，…”表示的缺失的条件应为（ ）
A. 甜果七个用四文钱，苦果九个用十一文钱
B. 甜果十一个用九文钱，苦果四个用七文钱
C. 甜果四个用七文钱，苦果十一个用九文钱
D. 甜果九个用十一文钱，苦果七个用四文钱

答案： D

11. [新考法 整体代入法] 若$\begin{cases}x = 2\\y = -1\end{cases}$是方程$ax - 2 = -by$的一组解，则$10a + 6 - 5b =$__________.

答案： 16 【点拨】把$\begin{cases}x = 2\\y = -1\end{cases}$代入$ax - 2 = -by$，得$2a - 2 = b$. 所以$2a - b = 2$. 所以$10a + 6 - 5b = 5(2a - b)+6 = 5×2 + 6 = 16$.