《2025年综合应用创新题典中点七年级数学下册冀教版》

1. 母题 教材P81练习T1 计算：$(-mn^{3})^{2}=$（ ）
A. $-m^{2}n^{6}$
B. $-mn^{6}$
C. $m^{2}n^{6}$
D. $mn^{6}$

答案： C

2. [2024石家庄模拟] 下列各图中，能直观解释“$(3a)^{2}=9a^{2}$”的是（ ）

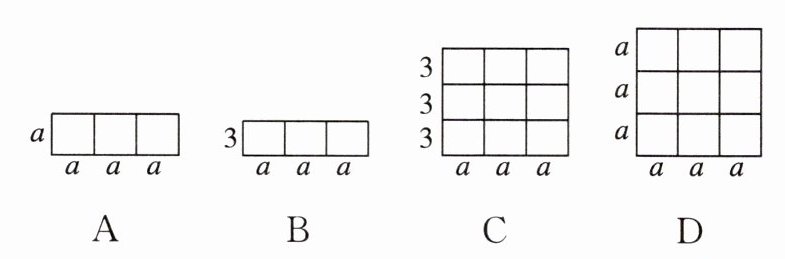
答案： D

3. 下列计算错误的是（ ）
A. $(2mn)^{2}=4m^{2}n^{2}$
B. $(-2mn)^{2}=4m^{2}n^{2}$
C. $(2m^{2}n^{2})^{3}=8m^{6}n^{6}$
D. $(-2m^{2}n^{2})^{3}=8m^{5}n^{5}$

答案： D

4. 计算$(-\frac{1}{7})^{2025}×7^{2026}$的值为（ ）
A. $-\frac{1}{7}$
B. $-7$
C. 7
D. $\frac{1}{7}$

答案： B　[点拨]原式=(−$\frac{1}{7}$)²025×72025×7=[(−$\frac{1}{7}$)×7]²025×7=(−1)²025×7=−1×7=−7,故选B.

5. 若$x^{n}y=-1$，则$(x^{3n}y^{3})^{2}=$_______.

答案： 1　[点拨]
∵$x^{n}y=−1$，
∴$(x^{n}y)^{3}=(−1)^{3}$，
∴$x^{3n}y^{3}=−1$，
∴$(x^{3n}y^{3})^{2}=(−1)^{2}=1$.

6. 母题 教材P80例3 计算：
（1）$(-x^{m}y^{3m})^{2}$；
（2）$6x^{3}·x^{7}-x^{4}·(-2x^{2})^{3}$.

答案： [解]
(1)原式$=(-1)^{2}x^{2m}y^{6m}=x^{2m}y^{6m}$；
(2)原式$=6x^{10}+x^{4}·8x^{6}=6x^{10}+8x^{10}=14x^{10}$.

7. 数$N = 2^{15}×5^{10}$是（ ）
A. 10位数
B. 11位数
C. 12位数
D. 13位数

答案： C　[点拨]$N=2^{15}×5^{10}=2^{5}×2^{10}×5^{10}=2^{5}×(2×5)^{10}=32×10^{10}=3.2×10^{11}$，
∴$N$是12位数.

8. 若$a = 2^{3}$，$b = 3^{2}$，用字母$a$，$b$表示$18^{18}$的结果为（ ）
A. $a^{4}b^{12}$
B. $a^{6}b^{14}$
C. $a^{6}b^{16}$
D. $a^{6}b^{18}$

答案： D　[点拨]$18^{18}=(2×3^{2})^{18}=2^{18}×b^{18}=2^{3×6}×b^{18}=a^{6}b^{18}$.

9. 新考法 新定义计算法 现规定一种新运算“※”：$a※b = b^{a}$. 如$3※2 = 2^{3}=8$，则$3※(-\frac{1}{2})=$_______，$4※(-2a^{3}b^{2})=$_______.

答案： −$\frac{1}{8}$;$16a^{12}b^{8}$　[点拨]$3※(-\frac{1}{2})=(-\frac{1}{2})^{3}=-\frac{1}{8}$；$4※(-2a^{3}b^{2})=(-2a^{3}b^{2})^{4}=16a^{12}b^{8}$.

10. 计算：$(-\frac{1}{10}×\frac{1}{9}×\frac{1}{8}×\cdots×\frac{1}{2}×1)^{10}×(10×9×8×\cdots×2×1)^{10}$.

答案： [解]原式$=(-\frac{1}{10}×10×\frac{1}{9}×9×\frac{1}{8}×8×\cdots×\frac{1}{2}×2×1×1)^{10}=(-1)^{10}=1$.

11. [2024南京鼓楼区期中]（1）若$2^{5}+2^{5}=2^{a}$，$3^{7}+3^{7}+3^{7}=3^{b}$，则$a + b =$_______；
（2）若$2^{m}×3^{n}=(4×27)^{7}$，求$m$，$n$；
（3）若$2^{p}=m$，$m^{q}=n$，$n^{r}=32$，求$pqr$.

答案： [解]
(1)14
(2)
∵$2^{m}×3^{n}=(4×27)^{7}=(2^{2}×3^{3})^{7}=2^{2×7}×3^{3×7}=2^{14}×3^{21}$，
∴$m = 14$，$n = 21$.
(3)
∵$2^{p}=m$，$m^{q}=n$，$n^{r}=32$，
∴$[(2^{p})^{q}]^{r}=32$，
∴$2^{pqr}=2^{5}$，
∴$pqr = 5$.

12. 新考法 逆向思维法 幂的运算性质在一定条件下具有可逆性，如：$(ab)^{m}=a^{m}b^{m}$（$m$为正整数），则$a^{m}b^{m}=(ab)^{m}$. 请运用所学知识解答下列问题：
（1）已知$2^{x + 3}×3^{x + 3}=36^{x - 2}$，求$x$的值；
（2）已知$3×2^{x + 1}×4^{x + 1}=192$，求$x$的值.

答案： [解]
(1)
∵$2^{x + 3}×3^{x + 3}=36^{x - 2}$，
∴$(2×3)^{x + 3}=(6^{2})^{x - 2}$，即$6^{x + 3}=6^{2(x - 2)}$，
∴$x + 3 = 2(x - 2)$，解得$x = 7$.
(2)
∵$3×2^{x + 1}×4^{x + 1}=192$，
∴$2^{x + 1}×2^{2(x + 1)} = 64$，
∴$2^{3(x + 1)} = 2^{6}$，
∴$3(x + 1) = 6$，解得$x = 1$.