《2025年综合应用创新题典中点七年级数学下册冀教版》

1. 母题 教材P130例1 在三角形ABC中，∠A = 40°，∠B = 60°，则∠C的度数为 （ ）
A. 20°
B. 50°
C. 80°
D. 100°

答案： C

2. 在△ABC中，∠A：∠B：∠C = 2：3：4，则∠A的度数为 （ ）
A. 35°
B. 40°
C. 70°
D. 110°

答案： B

3. 将一个含30°角的三角板和直尺如图放置，若∠1 = 50°，则∠2的度数是 （ ）

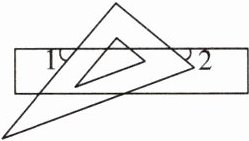
A. 30°
B. 40°
C. 50°
D. 60°

答案：
B　[点拨]如图,由题意得∠5 = 90°.
∵∠3 = ∠1 = 50°,∠3 + ∠4 + ∠5 = 180°,
∴∠4 = 90° - ∠3 = 40°.
∴∠2 = ∠4 = 40°.

4. 母题 教材P130大家谈谈 在探究说明“三角形的内角和是180°”时，作了如下四种辅助线，其中不能说明“三角形内角和是180°”的是（ ）

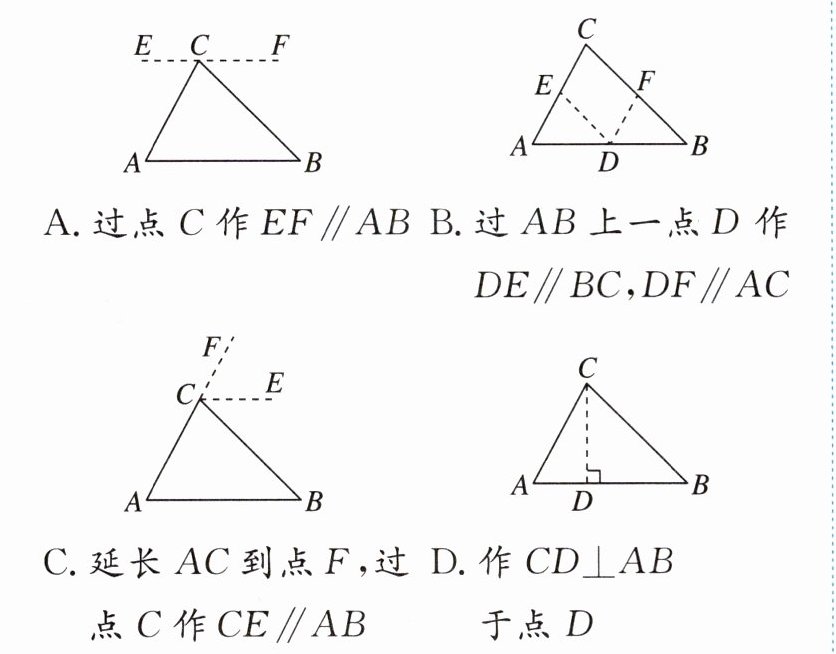
答案： D　[点拨]A. 由 EF//AB，得∠ECA = ∠A，∠FCB = ∠B.
∵∠ECA + ∠ACB + ∠FCB = 180°，
∴∠A + ∠ACB + ∠B = 180°，故 A 不符合题意. B. 由 ED//BC，得∠C = ∠AED，∠ADE = ∠B. 由 DF//AC，得∠A = ∠FDB，∠EDF = ∠AED，
∴∠C = ∠EDF.
∵∠ADE + ∠EDF + ∠FDB = 180°，
∴∠B + ∠C + ∠A = 180°，故 B 不符合题意. C. 由 CE//AB，得∠A = ∠FCE，∠B = ∠BCE.
∵∠FCE + ∠ECB + ∠ACB = 180°，
∴∠A + ∠B + ∠ACB = 180°，故 C 不符合题意. D. 由 CD⊥AB 于点 D，得∠ADC = ∠CDB = 90°. 无法证得三角形内角和是 180°，故 D 符合题意.

5. 如图，∠A = 70°，BP，CP分别平分∠ABC和∠ACB，则∠BPC的度数是 （ ）

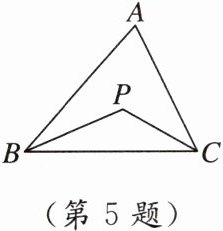
A. 125°
B. 115°
C. 110°
D. 35°

答案： A　[点拨]在△ABC 中，∠A = 70°，
∴∠ABC + ∠ACB = 180° - ∠A = 180° - 70° = 110°.
∵BP，CP 分别平分∠ABC 和∠ACB，
∴∠PBC = $\frac{1}{2}$∠ABC，∠PCB = $\frac{1}{2}$∠ACB. 在△PBC 中，∠BPC + ∠PBC + ∠PCB = 180°，
∴∠BPC = 180° - （∠PBC + ∠PCB） = 180° - $\frac{1}{2}$(∠ABC + ∠ACB)=180° - $\frac{1}{2}$×110° = 125°.

6. 如图，一块模板按规定AF，DE的延长线相交应成85°角，因交点不在模板上，不便于测量，工人师傅便连接AD，并测得∠FAD = 31°，∠ADE = 66°，这时AF，DE的延长线相交所成的角________规定（填“符合”或“不符合”）.

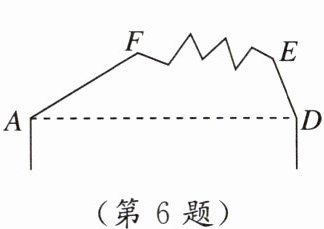
答案：
不符合　[点拨]延长 AF，DE 交于点 M，如图所示. 在△ADM 中，∠FAD = 31°，∠ADE = 66°，
∴∠AMD = 180° - ∠FAD - ∠ADE = 180° - 31° - 66° = 83°.
∵83°≠85°，
∴这时 AF，DE 的延长线相交所成的角不符合规定.

7. 如图，在△ABC中，BD平分∠ABC，AE⊥BC于点E，交BD于点F. 若∠ABC = 48°，求∠AFB的度数.

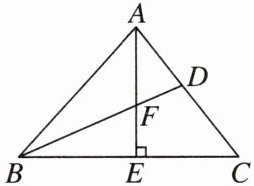
答案： [解]
∵BD 平分∠ABC，∠ABC = 48°，
∴∠ABD = ∠CBD = $\frac{1}{2}$∠ABC = 24°.
∵AE⊥BC，
∴∠BEF = 90°.
∴∠BFE = 180° - 90° - 24° = 66°.
∴∠AFB = 180° - 66° = 114°.

8. 新趋势 跨学科综合 如图，点P为某光源，一束平行于主光轴的光线经凸透镜折射后，其折射光线与一束经过光心O的光线相交于点Q，点F为焦点. 若∠PDQ = 158°，∠POM = 13°，则∠Q的度数为 （ ）

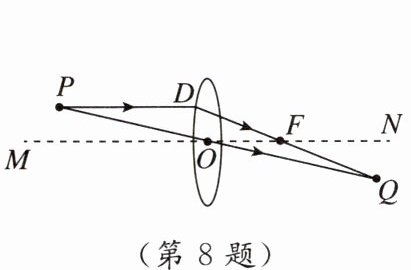
A. 15°
B. 19°
C. 9°
D. 25°

答案： C

9. 新考法 折叠法 如图，在△ABC中，∠C = 90°，∠B = 70°，点D，E分别在AB，AC上，将△ADE沿DE折叠，使点A落在F处. 则∠BDF - ∠CEF = （ ）

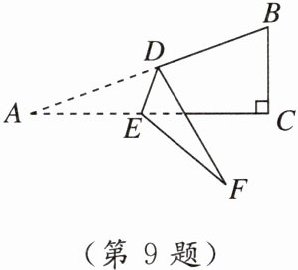
A. 20°
B. 30°
C. 40°
D. 50°

答案：
C　[点拨]如图,
∵∠C = 90°，∠B = 70°，
∴∠A = 20°. 由折叠可知∠1 = ∠2，∠3 = ∠DEF.
∵∠BDF + ∠1 + ∠2 = 180°，
∴∠BDF = 180° - 2∠1.
∵∠CEF + ∠CED = ∠DEF = ∠3，∠CED = ∠1 + ∠A，
∴∠CEF = ∠3 - ∠CED = 180° - （∠1 + ∠A） - ∠1 - ∠A = 180° - 2∠1 - 2∠A = 140° - 2∠1.
∴∠BDF - ∠CEF = 180° - 2∠1 - （140° - 2∠1） = 180° - 2∠1 - 140° + 2∠1 = 40°.