《2025年综合应用创新题典中点七年级数学下册冀教版》

1. 母题教材P41习题1 下面四个图形中，∠1与∠2是对顶角的是 ( )

答案： D

2. 在一张透明的纸上画一条直线l，在l外任取一点Q，并折出过点Q且与l垂直的直线，这样的直线能折出 ( )
A. 0条
B. 1条
C. 2条
D. 3条

答案： B

3. 下列命题中，是假命题的是 ( )
A. 对顶角相等
B. 正数大于负数
C. 垂线段最短
D. 若|a| = |b|，则a = b

答案： D

4. 如图，河道l的一侧有A，B两个村庄，现要铺设一条管道把河水引向A，B两村，下列四种方案中最节省材料的是 ( )

答案： B

5. 如图，三角形ABC是锐角三角形，过点C作CD⊥AB，垂足为D，则点C到直线AB的距离是 ( )

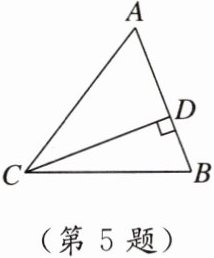
A. 线段CA的长
B. 线段CD
C. 线段AD的长
D. 线段CD的长

答案： D

6. 如图，下列说法错误的是 ( )

A. ∠1与∠2是同位角
B. ∠3与∠4是内错角
C. ∠1与∠3是同旁内角
D. 与∠A是同旁内角的角共有4个

答案： C 【点拨】A、∠1与∠2是同位角，原说法正确；B、∠3与∠4是内错角，原说法正确；C、∠1与∠3是内错角，原说法错误；D、与∠A是同旁内角的角共有4个，分别是∠1，∠2，∠ADE，∠AFB，原说法正确. 故选C.

7. 如图，直线AB，CD相交于点O，EO⊥AB，垂足为O. 若∠EOC = 38°，则∠AOD = ( )

A. 120°
B. 122°
C. 124°
D. 128°

答案： D 【点拨】因为EO⊥AB，所以∠AOE = 90°.因为∠EOC = 38°，所以∠AOC = 90° - 38° = 52°.所以∠AOD = 180° - 52° = 128°. 故选D.

8. 已知∠A的两边与∠B的两边互相垂直，且∠A比∠B的两倍小60°，则∠A = ( )
A. 60°
B. 100°
C. 60°或100°
D. 120°

答案：
C 【点拨】设∠B = α，则∠A = 2α - 60°，有两种情况：
①如图①，∠ACB = ∠AEB = 90°，
又因为∠AOC = ∠BOE，
所以∠A = ∠B. 所以2α - 60° = α.
所以α = 60°. 所以∠A = 60°;
　　　　　
②如图②，∠ACB = ∠ADB = 90°，连接CD.
因为∠CDA + ∠A + ∠ACD + ∠DCB + ∠B + ∠BDC = 180° + 180° = 360°，
所以∠A + ∠B + ∠ACB + ∠ADB = 360°.
所以∠A + ∠B = 180°.
所以2α - 60° + α = 180°. 所以α = 80°.
所以∠A = 2×80° - 60° = 100°.
综上，∠A = 60°或100°. 故选C.

9. 如图，一共有_______对同旁内角.

答案： 4

10. 如图，直线AB，CD相交于点O，OA平分∠EOC，若∠BOD = 30°，则∠EOD的度数为_______.

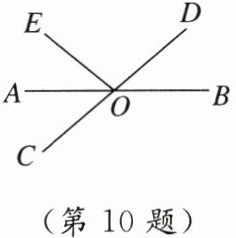
答案： 120° 【点拨】因为∠BOD = 30°，所以∠AOC = ∠BOD = 30°，因为OA平分∠EOC，所以∠EOC = 2∠AOC = 60°，所以∠EOD = 180° - ∠EOC = 180° - 60° = 120°.

11. 新考法 方程思想 如图，在三角形ABC中，∠ACB = 90°，AC = 5，BC = 12，AB = 13. 点P是线段AB上的一个动点，则CP的最小值为_______.

答案： $\frac{60}{13}$ 【点拨】在三角形ABC中，∠ACB = 90°，AC = 5，BC = 12，AB = 13，当CP⊥AB时，CP的值最小，此时，三角形ABC的面积 = $\frac{1}{2}$·AB·CP = $\frac{1}{2}$·AC·BC，所以13CP = 5×12，所以PC = $\frac{60}{13}$，即PC的最小值为$\frac{60}{13}$.

12. 新考法 发现规律法 观察下列图形：
如图①，两直线相交，最多1个交点；
如图②，三条直线相交最多有3个交点；
如图③，四条直线相交最多有6个交点；
…
那么十条直线相交交点个数最多为_______.

答案： 45 【点拨】两条直线相交，最多有1个交点；三条直线相交，最多有3个交点，即1 + 2 = 3；四条直线相交，最多有6个交点，即1 + 2 + 3 = 6；五条直线相交，最多有10个交点，即1 + 2 + 3 + 4 = 10；……所以十条直线相交交点个数最多为1 + 2 + 3 + 4 + … + 7 + 8 + 9 = 45.