《2025年综合应用创新题典中点七年级数学下册冀教版》

8. 直线AB//CD，BE - EC是一条折线段，BP平分∠ABE.
（1）如图①，若BP//CE，试说明：∠BEC + ∠DCE = 180°；
（2）CQ平分∠DCE，直线BP，CQ交于点F. 如图②，写出∠E和∠F的数量关系，并说明理由.

答案：
[解]
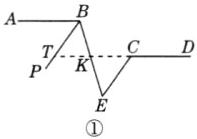
(1)延长DC交BE于点K,交BP于点T,如图①.
∵AB//CD,
∴∠ABT=∠BTK.
∵BP平分∠ABE,
∴∠ABP=∠PBK.
∴∠BTK=∠TBK.
∵BP//CE,
∴∠BTK=∠KCE,∠TBK=∠KEC;
∴∠KCE=∠KEC.
∵∠KCE+∠DCE=180°,
∴∠KEC+∠DCE=180°,即∠BEC+∠DCE=180°.

(2)∠E + 2∠F = 180°.理由如下:
延长AB交FQ于点M,延长DC交BE于点N,如图②.
∵CQ平分∠DCE,
∴∠DCQ = ∠ECQ.
设∠ABP = ∠EBP = α，∠DCQ = ∠ECQ = β，
∴∠FBM = ∠ABP = α，∠MBE = 180° - 2α，
∠NCE = 180° - 2β，∠FCN = ∠DCQ = β.
∵AB//DC，
∴∠CNE = ∠MBE = 180° - 2α，∠FMB = ∠NCF = β.
∴∠F = 180° - ∠FBM - ∠FMB = 180° - (α + β)，
∠E = 180° - ∠NCE - ∠CNE = 180° - (180° - 2β) - (180° - 2α) = 2(α + β) - 180°.
∴∠E + 180° = 2(180° - ∠F).
∴∠E + 2∠F = 180°.

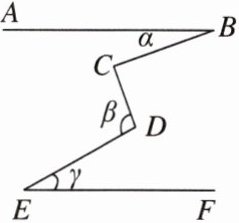
9. 如图，AB//EF，BC⊥CD，则∠α，∠β，∠γ之间的关系是 （ ）
A. ∠β = ∠α + ∠γ
B. ∠α + ∠β + ∠γ = 180°
C. ∠α + ∠β - ∠γ = 90°
D. ∠β + ∠γ - ∠α = 90°

答案：
9.C　[点拨]如图,分别过C,D作AB的平行线CM和DN.
∵AB//EF,
∴AB//CM//DN//EF.
∴∠α = ∠BCM，∠MCD = ∠NDC，∠NDE = ∠γ.
∴∠α + ∠β = ∠BCM + ∠CDN + ∠NDE = ∠BCM + ∠MCD + ∠γ.
∵BC⊥CD，
∴∠BCD = 90°.
∴∠α + ∠β = 90° + ∠γ，即∠α + ∠β - ∠γ = 90°. 故选C.

10. 新视角 项目探究题 小荣学习了角平分线的定义以及平行线的判定与性质的相关知识后，对角之间的关系进行了拓展探究. 如图①，直线AB//CD，直线AC是直线AB，CD的第三条截线，AK，CK分别是∠BAC，∠DCA的平分线，并且相交于点K.

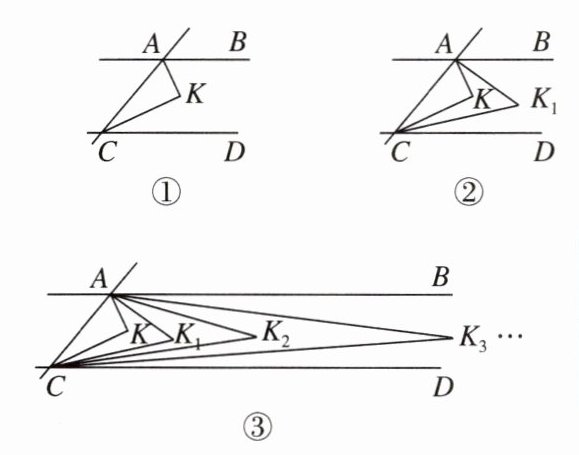
【问题解决】（1）∠BAC，∠DCA的平分线AK，CK所夹的∠K的度数为________；
【问题探究】（2）如图②，∠BAK，∠DCK的平分线相交于点K1，请写出∠AK1C与∠AKC之间的等量关系，并说明理由；
【拓展延伸】（3）在图③中作∠BAK1，∠DCK1的平分线相交于点K2，作∠BAK2，∠DCK2的平分线相交于点K3，以此类推，作∠BAK2025，∠DCK2025的平分线相交于点K2026，求出∠K2026的度数.

答案：
[解]
(1)90°
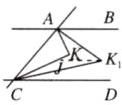
(2)∠AK₁C = $\frac{1}{2}$∠AKC. 理由如下:
如图，过点K₁作K₁J//AB.
∵AB//CD，K₁J//AB，
∴K₁J//AB//CD.
∴∠AK₁J = ∠BAK₁，∠JK₁C = ∠DCK₁.
∵∠BAK，∠DCK的平分线相交于点K₁，
∴∠BAK₁ = $\frac{1}{2}$∠BAK，∠DCK₁ = $\frac{1}{2}$∠DCK.
∴∠AK₁C = ∠BAK₁ + ∠DCK₁ = $\frac{1}{2}$(∠BAK + ∠DCK).
同理∠AKC = ∠BAK + ∠DCK，
∴∠AK₁C = $\frac{1}{2}$∠AKC.

(3)由
(2)可知∠K₁ = $\frac{1}{2}$∠K. 同理可得∠K₂ = $\frac{1}{2}$∠K₁ = ($\frac{1}{2}$)²∠K，∠K₃ = $\frac{1}{2}$∠K₂ = ($\frac{1}{2}$)³∠K，…，则∠Kₙ = ($\frac{1}{2}$)ⁿ∠K.
当n = 2026时，∠K₂₀₂₆ = ($\frac{1}{2}$)²⁰²⁶∠K = ($\frac{1}{2}$)²⁰²⁶×90°.

5. [2024廊坊校级月考] 下列各图中的MA1与NAn + 1平行.

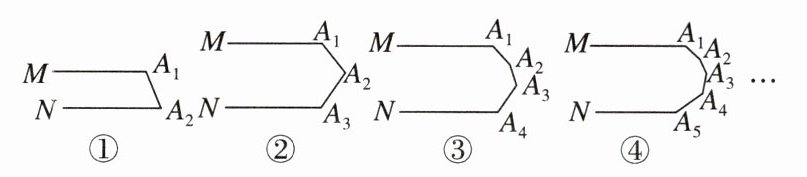
（1）图①中的∠A1 + ∠A2 = ________，图②中的∠A1 + ∠A2 + ∠A3 = ________，图③中的∠A1 + ∠A2 + ∠A3 + ∠A4 = ________；
（2）第（n - 1）个图中的∠A1 + ∠A2 + ∠A3 + … + ∠An = ________.

答案：
(1)180°;360°;540°　
(2)180°(n−1)