《2025年综合应用创新题典中点七年级数学下册冀教版》

1. 下列方程组中，是二元一次方程组的是( )
A. $\begin{cases}xy = 5,\\y = 0\end{cases}$
B. $\begin{cases}x - 5y = 1,\\x + y = 3\end{cases}$
C. $\begin{cases}x^{2}-y = 6,\\x + 3y = 0\end{cases}$
D. $\begin{cases}2x + y = 1,\\x + y + 3z = 2\end{cases}$

答案： B

2. 若$\begin{cases}x = 5,\\y = - 2\end{cases}$是关于$x$，$y$的方程$2x - 3y - 4a = 0$的一组解，则$a$的值为( )
A. - 2
B. 1
C. 2
D. 4

答案： D

3. 二元一次方程$x + y = 4$的正整数解有( )
A. 1组
B. 2组
C. 3组
D. 4组

答案： C

4. 已知$x$，$y$满足方程组$\begin{cases}2x - y = 4,\\x + 4y = - 1,\end{cases}$则$x + y$的值是( )
A. 1
B. 3
C. 7
D. 9

答案： A

5. [2024廊坊校级月考] 若$5x^{5}y^{2m + n}$与$-7x^{3m + 2n}y^{6}$是同类项，则$n - m =$( )
A. 1
B. - 1
C. 2
D. 3

答案： 因为$5x^{5}y^{2m + 3n}$与$-7x^{3m + 2n}y^{6}$是同类项，所以$\begin{cases}3m + 2n = 5,①\\2m + 3n = 6,②\end{cases}$，② - ①，得$n - m = 1$。

6. 真实情境题 航天科技 为了庆祝2024年11月30日，我国自主研发的首型4米级运载火箭长征十二号首飞成功，某学校组织学生开展有关航空航天的知识竞赛. 竞赛共有20道题，规定：每答对一道题得5分，每答错一道题扣3分，不答的题得1分. 已知杭杭同学这次竞赛成绩为60分. 设杭杭同学答对了$x$道题，答错了$y$道题，则有( )
A. $x - y = 10$
B. $5x - 3y = 60$
C. $3x - y = 40$
D. $x + y = 20$

答案： 依题意得$5x - 3y+(20 - x - y)=60$，即$x - y = 10$。故选A。

7. 已知方程组$\begin{cases}5x + y = 3,\\px + 5y = 2\end{cases}$和$\begin{cases}x - 2y = 5,\\5x + qy = 7\end{cases}$有相同的解，则$p$，$q$的值为( )
A. 1，- 2
B. 1，2
C. 12，1
D. 12，- 1

答案： 因为方程组$\begin{cases}5x + y = 3,\\px + 5y = 2\end{cases}$和$\begin{cases}x - 2y = 5,\\5x + qy = 7\end{cases}$有相同的解，所以它们的解是方程组$\begin{cases}5x + y = 3,\\x - 2y = 5\end{cases}$的解，解方程组$\begin{cases}5x + y = 3,\\x - 2y = 5\end{cases}$，得$\begin{cases}x = 1,\\y = - 2\end{cases}$，将$\begin{cases}x = 1,\\y = - 2\end{cases}$代入$\begin{cases}px + 5y = 2,\\5x + qy = 7\end{cases}$，解得$\begin{cases}p = 12,\\q = - 1\end{cases}$。故选D。

8. 某社区为了打造“书香社区”，丰富小区居民的业余文化生活，计划出资500元全部用于采购A，B，C三种图书，A种每本30元，B种每本25元，C种每本20元，其中A种图书至少买5本，最多买6本(三种图书都要买)，此次采购的方案有( )
A. 5种
B. 6种
C. 7种
D. 8种

答案： 当购买5本A种图书时，设购买$x$本B种图书，$y$本C种图书。根据题意，得$30×5 + 25x + 20y = 500$，整理得$x = 14-\frac{4}{5}y$。因为$x$，$y$均为正整数，所以$\begin{cases}x = 10,\\y = 5\end{cases}$或$\begin{cases}x = 6,\\y = 10\end{cases}$或$\begin{cases}x = 2,\\y = 15\end{cases}$。所以当购买5本A种图书时，有3种采购方案。当购买6本A种图书时，设购买$m$本B种图书，$n$本C种图书。根据题意，得$30×6 + 25m + 20n = 500$，整理得$n = 16-\frac{5}{4}m$。因为$m$，$n$均为正整数，所以$\begin{cases}m = 4,\\n = 11\end{cases}$或$\begin{cases}m = 8,\\n = 6\end{cases}$或$\begin{cases}m = 12,\\n = 1\end{cases}$。所以当购买6本A种图书时，有3种采购方案。综上，此次采购的方案有$3 + 3 = 6$（种）。

9. [2024石家庄校级期中] 已知$3x - 7y = 41$，用含$x$的代数式表示$y$可得________.

答案： $y=\frac{3x - 41}{7}$

10. 已知$(x - 2y)^{2}+\vert5x - 7y - 2\vert = 0$，则$x =$________，$y =$________.

答案： $\frac{4}{3}$;$\frac{2}{3}$

11. 解方程组$\begin{cases}ax + by = 2,\\cx + 7y = 8\end{cases}$时，甲同学正确解得$\begin{cases}x = 2,\\y = 2,\end{cases}$乙同学因把$c$看错而得到$\begin{cases}x = - 1,\\y = 3,\end{cases}$则$a =$________，$b =$________，$c =$________.

答案： 0.25;0.75;−3

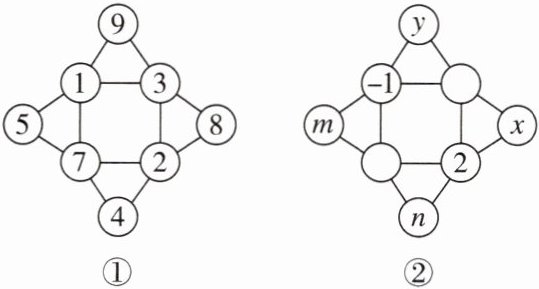
12. 新考向 数学文化 “幻方”最早记载于春秋时期的《大戴礼》中，现将1，2，3，4，5，7，8，9这8个数字填入如图①所示的“幻方”中，使得每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等. 现有如图②所示的“幻方”，则$(y - x)^{m - n}=$________.

答案： 27　[点拨]由题知，$y+( - 1)=x + 2$，整理得$y - x = 3$，$m+( - 1)=n + 2$，整理得$m - n = 3$，将$y - x = 3$，$m - n = 3$代入$(y - x)^{m - n}$中，有$(y - x)^{m - n}=3^{3}=27$。

13. (12分)解下列二元一次方程组：
(1)[2024苏州] $\begin{cases}2x + y = 7,\\2x - 3y = 3;\end{cases}$
(2)$\begin{cases}\frac{x + y}{2}+\frac{x - y}{3}= 6,\\4(x + y)-5(x - y)= 2.\end{cases}$

答案： [解]
(1)$\begin{cases}2x + y = 7,①\\2x - 3y = 3,②\end{cases}$
① - ②，得$4y = 4$，解得$y = 1$，将$y = 1$代入①，得$x = 3$，则原方程组的解为$\begin{cases}x = 3,\\y = 1\end{cases}$。
(2)原方程组可化为$\begin{cases}5x + y = 36,①\\-x + 9y = 2,②\end{cases}$
②×5，得$-5x + 45y = 10$，③
① + ③，得$46y = 46$，解得$y = 1$，把$y = 1$代入②，得$x = 7$，所以原方程组的解是$\begin{cases}x = 7,\\y = 1\end{cases}$。