第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
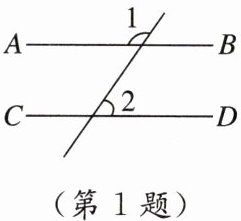
1. [2024·重庆 母题:教材P56练习T1]如图,AB//CD,若∠1 = 125°,则∠2的度数为( )
A. 35° B. 45° C. 55° D. 125°
A. 35° B. 45° C. 55° D. 125°

答案:
C
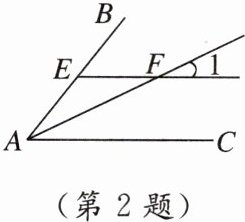
2. [2024承德期末]如图,AF是∠BAC的平分线,EF//AC交AB于点E,若∠1 = 35°,则∠BEF的度数为( )
A. 35° B. 60° C. 70° D. 80°
A. 35° B. 60° C. 70° D. 80°

答案:
C
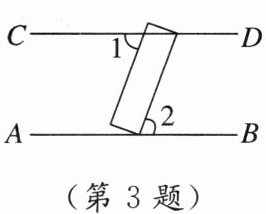
3. [2024保定期末]一把直尺按如图所示的方式摆放,AB//CD,且∠1 = 70°,则∠2的度数是( )
A. 70° B. 60° C. 30° D. 80°
A. 70° B. 60° C. 30° D. 80°

答案:
A
4. 如图,直角三角形ABC中,∠ACB = 90°,DE过点C且平行于AB,若∠BCE = 35°,则∠A的度数为_______.
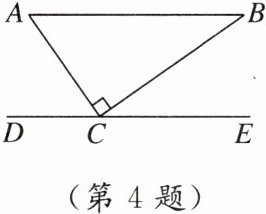

答案:
$55^{\circ}$
5. 如图,AC//ED,AB//FD,∠A = 65°,则∠EDF的度数为_______.


答案:
$65^{\circ}$
6. [2024衡水校级月考]如图,已知l1//l2,直线l与l1,l2分别相交于C,D两点,把一块含30°角的三角板按如图位置摆放. 若∠1 = 130°,则∠2 = _______.
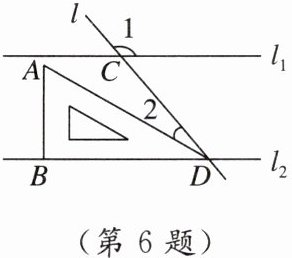

答案:
$20^{\circ}$
7. 某县积极推进“乡村振兴计划”,要对一段水渠进行扩建. 如图,已知现有水渠从A地沿北偏东50°的方向到B地,又从B地沿北偏西20°的方向到C地. 现要从C地出发修建一段新渠CD,使CD//AB,求∠BCD的度数.
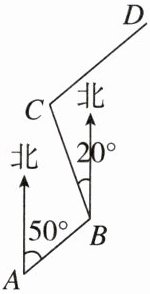

答案:
【解】$\because B$地在$A$地的北偏东$50^{\circ}$方向上,$C$地在$B$地北偏西$20^{\circ}$方向上,$\therefore\angle ABC = 180^{\circ}-50^{\circ}-20^{\circ}=110^{\circ}$。
$\because CD// AB$,$\therefore\angle BCD=\angle ABC = 110^{\circ}$。
$\because CD// AB$,$\therefore\angle BCD=\angle ABC = 110^{\circ}$。
8. 如图,直线l1//l2,直线AD与l1,l2分别相交于点B,C,下列式子中表述正确的是( )
A. γ = 2α + β B. γ = α + 2β
C. γ = α + β D. γ = α + β - 180°
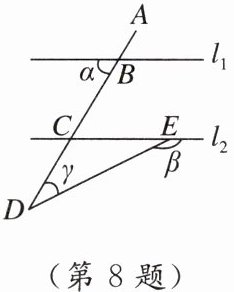
A. γ = 2α + β B. γ = α + 2β
C. γ = α + β D. γ = α + β - 180°

答案:
D 【点拨】$\because l_{1}// l_{2}$,$\therefore\angle ACE=\alpha$。$\therefore\angle DCE = 180^{\circ}-\alpha$。
$\because\angle CED = 180^{\circ}-\beta$,$\therefore 180^{\circ}-\alpha+180^{\circ}-\beta+\gamma = 180^{\circ}$。
$\therefore\gamma=\alpha+\beta - 180^{\circ}$。故选D。
$\because\angle CED = 180^{\circ}-\beta$,$\therefore 180^{\circ}-\alpha+180^{\circ}-\beta+\gamma = 180^{\circ}$。
$\therefore\gamma=\alpha+\beta - 180^{\circ}$。故选D。
9. [新趋势 跨学科综合]如图,一束光线AB先后经平面镜OM,ON反射后,光线CD与AB平行,已知∠ABM = 35°,∠OBC = ∠ABM,∠OCB = ∠DCN,则∠DCN的度数是_______.
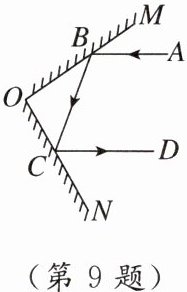

答案:
$55^{\circ}$ 【点拨】$\because\angle ABM = 35^{\circ}$,$\angle OBC=\angle ABM$,
$\therefore\angle OBC=\angle ABM = 35^{\circ}$。$\therefore\angle ABC = 180^{\circ}-35^{\circ}-35^{\circ}=110^{\circ}$。$\because AB// CD$,$\therefore\angle BCD+\angle ABC = 180^{\circ}$,$\therefore\angle BCD = 70^{\circ}$。$\because\angle OCB=\angle DCN$,$\therefore\angle DCN=(180^{\circ}-\angle BCD)\div2 = 55^{\circ}$。
$\therefore\angle OBC=\angle ABM = 35^{\circ}$。$\therefore\angle ABC = 180^{\circ}-35^{\circ}-35^{\circ}=110^{\circ}$。$\because AB// CD$,$\therefore\angle BCD+\angle ABC = 180^{\circ}$,$\therefore\angle BCD = 70^{\circ}$。$\because\angle OCB=\angle DCN$,$\therefore\angle DCN=(180^{\circ}-\angle BCD)\div2 = 55^{\circ}$。
查看更多完整答案,请扫码查看


