《2025年综合应用创新题典中点七年级数学下册冀教版》

1. [2024宿迁校级期中] 下列各式中不能用平方差公式计算的是 （ ）
A. (2a + b)(b - 2a)
B. (2a - b)(-2a - b)
C. (-2a - b)(-2a + b)
D. (2a - b)(-2a + b)

答案： D

2. [2024廊坊模拟] 下列运算正确的是 （ ）
A. $x^{2}+y^{2}=(x + y)^{2}$
B. $(x - y)^{2}=(y - x)^{2}$
C. $(-3x^{2}y^{3})^{2}=6x^{4}y^{6}$
D. $(x - y)(-y - x)=x^{2}-y^{2}$

答案： B

3. [2024保定校级月考] 如图，边长为$(a + 3)$的正方形纸片剪出一个边长为$a$的正方形之后，将剩余部分剪拼成一个长方形（不重叠，无缝隙），若拼成的长方形一边长为3，则另一边长是 （ ）

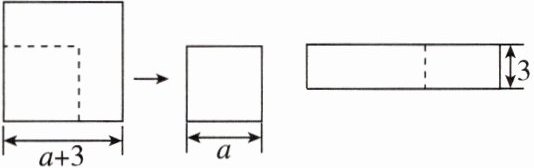
A. $2a + 3$
B. $2a + 6$
C. $a + 3$
D. $a + 6$

答案： A

4. [新考法 整体代入法] 已知$(x + 2)(x - 2)-2x = 1$，则$2x^{2}-4x + 3$的值为 （ ）
A. 13
B. 3
C. -3
D. 5

答案： A [点拨]
∵(x + 2)(x - 2)-2x = 1，
∴x² - 4 - 2x = 1.
∴x² - 2x = 5.
∴2x² - 4x + 3 = 2(x² - 2x)+3 = 2×5 + 3 = 10 + 3 = 13.

5. 已知$M = 2026^{2}$，$N = 2025×2027$，则$M$与$N$的大小关系是 （ ）
A. $M＞N$
B. $M＜N$
C. $M = N$
D. 不能确定

答案： A [点拨]
∵M = 2026²，N = 2025×2027=(2026 - 1)(2026 + 1)=2026² - 1，
∴M＞N.

6. [2024秦皇岛期末] 若$x^{2}-y^{2}=20$，$x - y = 4$，则$x + y =$_______.

答案： 5

7. [2024·苏州校级模拟] [新考法 整体代入法] 已知$3m - n = 1$，则$9m^{2}-n^{2}-2n$的值为_______.

答案： 1 [点拨]
∵3m - n = 1，
∴原式=(3m + n)(3m - n)-2n = 3m + n - 2n = 3m - n = 1.

8. 计算：
(1)$(-2a^{2}+5b)(-2a^{2}-5b)$；
(2)$59\frac{4}{5}×60\frac{1}{5}$.

答案： [解]
(1)原式=(-2a²)² - (5b)² = 4a⁴ - 25b².
(2)原式=(60 - $\frac{1}{5}$)×(60 + $\frac{1}{5}$)=60² - ($\frac{1}{5}$)² = 3600 - $\frac{1}{25}$ = 3599$\frac{24}{25}$.

9. [母题 教材P96习题T3] 先化简，再求值：$(2x - 1)(2x + 1)-(x - 2)(x + 3)-2x(x - 1)$，其中$x = -2$.

答案： [解](2x - 1)(2x + 1)-(x - 2)(x + 3)-2x(x - 1)
　=4x² - 1-(x² + x - 6)-2x² + 2x
　=4x² - 1 - x² - x + 6 - 2x² + 2x
　=x² + x + 5.
　当x = - 2时，原式=(-2)² + (-2)+5 = 4 - 2 + 5 = 7.

10. [2024石家庄藁城区模拟] 当$n$为正整数时，代数式$(2n + 1)^{2}-(2n - 1)^{2}$一定是下面哪个数的倍数 （ ）
A. 3
B. 5
C. 7
D. 8

答案： D [点拨](2n + 1)² - (2n - 1)²=[(2n + 1)-(2n - 1)][(2n + 1)+(2n - 1)] = 8n，故当n是正整数时，(2n + 1)² - (2n - 1)²是8的倍数.故选D.

11. 若$(a^{2}+b^{2}-1)(a^{2}+b^{2}+1)=8$，则$a^{2}+b^{2}=$ （ ）
A. 3
B. 6
C. ±3
D. ±6

答案： A [点拨]若(a² + b² - 1)(a² + b² + 1)=8，则(a² + b²)² = 9，因为a² + b²≥0，所以a² + b² = 3.故选A.

12. 如图，若大正方形与小正方形的面积之差是30，则阴影部分的面积是 （ ）

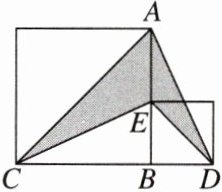
A. 15
B. 20
C. 30
D. 35

答案： A [点拨]设大正方形的边长为x，小正方形的边长为y，则AE = x - y.由题意可知x² - y² = 30.阴影部分的面积是$\frac{1}{2}$AE·BC + $\frac{1}{2}$AE·DB = $\frac{1}{2}$(x - y)·x + $\frac{1}{2}$(x - y)·y = $\frac{1}{2}$(x - y)(x + y) = $\frac{1}{2}$(x² - y²) = $\frac{1}{2}$×30 = 15.