《2025年综合应用创新题典中点七年级数学下册冀教版》

9. 如图，请猜想∠A+∠B+∠C+∠D+∠E+∠F的度数，并说明你的理由.

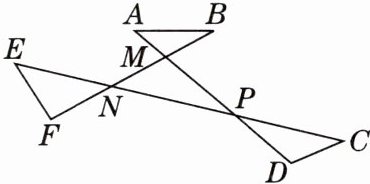
答案： [解]∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 360°.
理由:由题易得∠A + ∠B + ∠AMB + ∠C + ∠D + ∠CPD + ∠E + ∠F + ∠ENF = 180° + 180° + 180° = 540°.
∵∠AMB = ∠NMP，∠CPD = ∠MPN，∠ENF = ∠MNP，∠NMP + ∠MPN + ∠MNP = 180°，
∴∠AMB + ∠CPD + ∠ENF = 180°.
∴∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 540° - 180° = 360°.

10. [2024邢台校级月考] 如图，在△ABC中，AD是△ABC的角平分线，P为线段AD上的一个动点，PE⊥AD交BC的延长线于点E.
(1)若∠B=30°，∠ACB=80°，求∠E的度数；
(2)当P点在线段AD上运动时，若∠E是锐角，试说明∠E=$\frac{1}{2}$(∠ACB - ∠B).

答案：
[解]
(1)
∵∠B = 30°，∠ACB = 80°，
∴∠BAC = 70°.
又
∵AD 平分∠BAC，
∴∠DAC = 35°.
∴∠ADC = 65°.
∵PE⊥AD，
∴∠DPE = 90°.
∴∠E = 25°.
(2)如图，设∠B = n°，∠ACB = m°. 则∠BAC = (180 - n - m)°.
∵AD 平分∠BAC，
∴∠1 = $\frac{1}{2}$∠BAC = $\frac{1}{2}$(180 - n - m)°.
∴∠2 = ∠B + ∠1 = n° + $\frac{1}{2}$(180 - n - m)° = 90° + $\frac{1}{2}$n° - $\frac{1}{2}$m°.
∵PE⊥AD，
∴∠DPE = 90°.
∴∠E = 90° - (90° + $\frac{1}{2}$n° - $\frac{1}{2}$m°) = $\frac{1}{2}$(m° - n°) = $\frac{1}{2}$(∠ACB - ∠B).

11. 已知a，b是等腰三角形的两条边长，且|a - 4|+(b - 8)² = 0，求这个三角形的周长.

答案： [解]
∵|a - 4| + (b - 8)² = 0，
∴a - 4 = 0，b - 8 = 0.
∴a = 4，b = 8.
当 a 为腰，b 为底时，不能构成三角形；
当 a 为底，b 为腰时，等腰三角形的周长为 8 + 8 + 4 = 20.
综上，这个三角形的周长为 20.

12. 母题教材P141复习题T11 如图，在△ABC中，分别延长△ABC的边AB，AC到点D，E，∠CBD与∠BCE的平分线相交于点P，爱动脑筋的小明在写作业时发现如下规律：
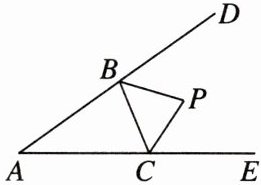
a. 若∠A=40°，则∠P=70°=90° - $\frac{40°}{2}$；
b. 若∠A=90°，则∠P=45°=90° - $\frac{90°}{2}$；
c. 若∠A=110°，则∠P=35°=90° - $\frac{110°}{2}$；
….
(1)根据上述规律，若∠A=160°，则∠P=________；
(2)∠P=________（用含∠A的式子表示）；
(3)试说明(2)中的结论.

答案： [解]
(1)10°
(2)$90°-\frac{1}{2}$∠A
(3)在△ABC 中，∠ABC + ∠ACB = 180° - ∠A，
∵∠ABC = 180° - ∠DBC，∠ACB = 180° - ∠BCE，
∴360° - (∠DBC + ∠BCE) = 180° - ∠A，即∠DBC + ∠BCE = 180° + ∠A.
∵BP 平分∠DBC，CP 平分∠BCE，
∴∠PBC = $\frac{1}{2}$∠DBC，∠PCB = $\frac{1}{2}$∠BCE.
∴∠PBC + ∠PCB = $\frac{1}{2}$(∠DBC + ∠BCE).
在△PBC 中，∠P = 180° - (∠PBC + ∠PCB) = 180° - $\frac{1}{2}$(∠DBC + ∠BCE) = 90° - $\frac{1}{2}$∠A.