第105页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. [2024秦皇岛模拟] 如图,若∠1 = 40°,则∠2的度数为 ( )
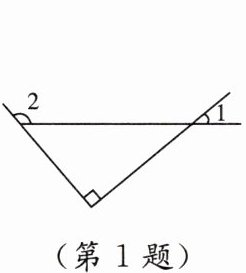
A. 120° B. 130° C. 140° D. 150°

A. 120° B. 130° C. 140° D. 150°
答案:
B
2. 如图,被信封遮住的三角形是 ( )
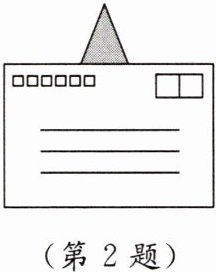
A. 锐角三角形
B. 直角三角形
C. 钝角三角形
D. 以上都有可能

A. 锐角三角形
B. 直角三角形
C. 钝角三角形
D. 以上都有可能
答案:
D
3. [2024廊坊校级月考] 如图,在△ABC中,点D,E在射线BA上,则∠1,∠2,∠B之间的大小关系为 ( )
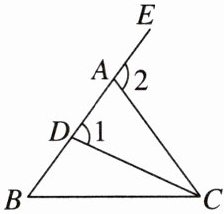
A. ∠1<∠2<∠B
B. ∠B<∠2<∠1
C. ∠1<∠B<∠2
D. ∠B<∠1<∠2

A. ∠1<∠2<∠B
B. ∠B<∠2<∠1
C. ∠1<∠B<∠2
D. ∠B<∠1<∠2
答案:
D
4. [2024石家庄藁城区期末] 将一副三角板按图中方式叠放,则∠α的度数为________.
(第4题)

(第4题)

答案:
$75^{\circ}$
5. 新趋势 跨学科综合 如图,一束平行于水平面的光线经过凹透镜折射后与另一束穿过光心O的光线相交于点B,若∠BDE = 45°,∠ABO = 15°,则∠MAB =________°.
(第5题)

(第5题)

答案:
150 [点拨]如图,延长MA交直线DO于点G,由题意得MA//DE,又
∵∠BDE = 45°,
∴∠MGD = ∠BDE = 45°. 又
∵∠ABO = 15°,
∴∠BAG = ∠MGD - ∠ABO = 45° - 15° = 30°.
∴∠MAB = 180° - ∠BAG = 180° - 30° = 150°.

150 [点拨]如图,延长MA交直线DO于点G,由题意得MA//DE,又
∵∠BDE = 45°,
∴∠MGD = ∠BDE = 45°. 又
∵∠ABO = 15°,
∴∠BAG = ∠MGD - ∠ABO = 45° - 15° = 30°.
∴∠MAB = 180° - ∠BAG = 180° - 30° = 150°.

6. 母题教材P134习题T2 三角形的一个外角等于与它相邻的内角的5倍,又等于与它不相邻的一个内角的3倍,则该三角形各角的度数为__________.
答案:
$30^{\circ},50^{\circ},100^{\circ}$ [点拨]设和外角相邻的内角为$x^{\circ}$,则外角为$5x^{\circ}$,
∴$x + 5x = 180$,解得$x = 30$.
∴外角为$30^{\circ}×5 = 150^{\circ}$.
∴与外角不相邻的一个内角为$150^{\circ}÷3 = 50^{\circ}$.
∴另外一个内角为$150^{\circ} - 50^{\circ} = 100^{\circ}$.
∴该三角形各角的度数为$30^{\circ},50^{\circ},100^{\circ}$.
∴$x + 5x = 180$,解得$x = 30$.
∴外角为$30^{\circ}×5 = 150^{\circ}$.
∴与外角不相邻的一个内角为$150^{\circ}÷3 = 50^{\circ}$.
∴另外一个内角为$150^{\circ} - 50^{\circ} = 100^{\circ}$.
∴该三角形各角的度数为$30^{\circ},50^{\circ},100^{\circ}$.
7. [2024唐山期中] 如图,在梯形纸片ABCD中,∠B = 132°.
(1)∠C = ________;
(2)剪掉梯形纸片中的∠C,并使剪痕EF⊥BC,则∠DFE = ________.
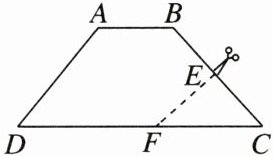
(1)∠C = ________;
(2)剪掉梯形纸片中的∠C,并使剪痕EF⊥BC,则∠DFE = ________.

答案:
(1) $48^{\circ}$ [点拨]
∵四边形ABCD为梯形,
∴AB//CD.
∴∠B + ∠C = 180°. 又
∵∠B = 132°,
∴∠C = 180° - 132° = 48°.
(2) $138^{\circ}$ [点拨]
∵EF⊥BC,
∴∠FEC = 90°.
∴∠DFE = ∠FEC + ∠C = 90° + 48° = 138°.
(1) $48^{\circ}$ [点拨]
∵四边形ABCD为梯形,
∴AB//CD.
∴∠B + ∠C = 180°. 又
∵∠B = 132°,
∴∠C = 180° - 132° = 48°.
(2) $138^{\circ}$ [点拨]
∵EF⊥BC,
∴∠FEC = 90°.
∴∠DFE = ∠FEC + ∠C = 90° + 48° = 138°.
8. 如图,在△ABC中,AD平分∠BAC,P为线段AD上一点,PE⊥AD交BC的延长线于点E,若∠B = 35°,∠ACB = 85°,求∠E的度数.
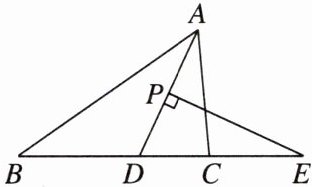

答案:
[解]
∵∠B = 35°,∠ACB = 85°,
∴∠BAC = 180° - ∠B - ∠ACB = 60°.
又
∵AD平分∠BAC,
∴∠DAC = ∠DAB=$\frac{1}{2}$∠BAC = 30°.
∴∠ADC = ∠B + ∠BAD = 65°.
∵PE⊥AD,
∴∠APE = 90°.
∴∠E = 90° - ∠ADC = 25°.
∵∠B = 35°,∠ACB = 85°,
∴∠BAC = 180° - ∠B - ∠ACB = 60°.
又
∵AD平分∠BAC,
∴∠DAC = ∠DAB=$\frac{1}{2}$∠BAC = 30°.
∴∠ADC = ∠B + ∠BAD = 65°.
∵PE⊥AD,
∴∠APE = 90°.
∴∠E = 90° - ∠ADC = 25°.
9. 如图,下列说法中错误的是 ( )

A. ∠B>∠ACD
B. ∠B+∠ACB = 180°-∠A
C. ∠B+∠ACB<180°
D. ∠HEC>∠B

A. ∠B>∠ACD
B. ∠B+∠ACB = 180°-∠A
C. ∠B+∠ACB<180°
D. ∠HEC>∠B
答案:
A
10. [2024南京六合区校级期中] 如图,在△ABC中,∠ACB = 90°,沿CD折叠△CBD,使点B恰好落在AC边上的E处.若∠A = 30°,则∠ADE = ________.
(第10题)

(第10题)

答案:
$30^{\circ}$ [点拨]
∵∠ACB = 90°,∠A = 30°,
∴∠B = 90° - 30° = 60°.
∵沿CD折叠△CBD,使点B恰好落在AC边上的E处,
∴∠DEC = ∠B = 60°.
∵∠DEC = ∠A + ∠ADE,
∴∠ADE = 60° - 30° = 30°.
∵∠ACB = 90°,∠A = 30°,
∴∠B = 90° - 30° = 60°.
∵沿CD折叠△CBD,使点B恰好落在AC边上的E处,
∴∠DEC = ∠B = 60°.
∵∠DEC = ∠A + ∠ADE,
∴∠ADE = 60° - 30° = 30°.
11. 新考法 整体求值法 如图,D,E,F分别是△ABC三边延长线上的点,若∠D+∠E+∠F = 107°,则∠1+∠2+∠3的度数为 ( )
A. 73° B. 63° C. 83° D. 93°
(第11题)

A. 73° B. 63° C. 83° D. 93°
(第11题)

答案:
A [点拨]
∵∠D + ∠3 = ∠CAB,∠E + ∠1 = ∠ABC,∠F + ∠2 = ∠ACB,
∴∠D + ∠E + ∠F + ∠1 + ∠2 + ∠3 = ∠CAB + ∠ABC + ∠ACB = 180°. 又
∵∠D + ∠E + ∠F = 107°,
∴∠1 + ∠2 + ∠3 = 73°.
∵∠D + ∠3 = ∠CAB,∠E + ∠1 = ∠ABC,∠F + ∠2 = ∠ACB,
∴∠D + ∠E + ∠F + ∠1 + ∠2 + ∠3 = ∠CAB + ∠ABC + ∠ACB = 180°. 又
∵∠D + ∠E + ∠F = 107°,
∴∠1 + ∠2 + ∠3 = 73°.
查看更多完整答案,请扫码查看


