《2025年综合应用创新题典中点七年级数学下册冀教版》

11. 新趋势 跨学科综合 如图，当光线从空气射入水中时，光线的传播方向发生了改变，这就是光的折射现象. 若∠1 = 42°，∠2 = 28°，则光的传播方向改变了________.

答案： $14^{\circ}$

12. 新考法 分类讨论法 在直线AB上任取一点E，过点E作射线EC，ED，使EC⊥ED. 如果∠AEC = 40°，那么∠BED的度数为________.

答案：
$50^{\circ}$或$130^{\circ}$ [点拨]当$EC$，$ED$在$AB$的同一侧时，如图①。

因为$EC\perp ED$，所以$\angle CED = 90^{\circ}$。因为$\angle AEC = 40^{\circ}$，所以$\angle BED=180^{\circ}-\angle CED-\angle AEC = 50^{\circ}$；当$EC$，$ED$在$AB$的两侧时，如图②。因为$EC\perp ED$，$\angle AEC = 40^{\circ}$，所以$\angle AED = 50^{\circ}$。所以$\angle BED=180^{\circ}-\angle AED = 130^{\circ}$。综上，$\angle BED$的度数为$50^{\circ}$或$130^{\circ}$。

13. [2024秦皇岛期中] 如图，直线AB，CD相交于点O，OE平分∠AOD，OG平分∠BOD，∠BOD = α，H是OA上的一点.
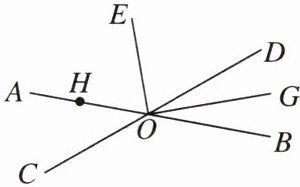
(1)过点H作直线CD的垂线HF，垂足为F.
(2)在(1)的基础上，求∠FHO的度数（用含α的式子表示）.
(3)探究∠EOG的大小和∠BOD的大小是否有关？若有，请写出∠EOG的大小和∠BOD的大小关系；若没有，请说明理由.

答案：
[解]
(1)如图，$HF$即为所作。

(2)因为$HF\perp CD$，所以$\angle OFH = 90^{\circ}$。因为$\angle HOE=\angle BOD=\alpha$，所以$\angle FHO=180^{\circ}-\angle OFH-\angle HOE = 90^{\circ}-\alpha$。
(3)$\angle EOG$的大小和$\angle BOD$的大小没有关系。理由如下：因为直线$AB$，$CD$相交于点$O$，所以$\angle AOB = 180^{\circ}$。因为$OE$平分$\angle AOD$，$OG$平分$\angle BOD$，所以$\angle EOD=\frac{1}{2}\angle AOD$，$\angle GOD=\frac{1}{2}\angle BOD$。所以$\angle EOD+\angle GOD=\frac{1}{2}(\angle AOD+\angle BOD)=\frac{1}{2}\times180^{\circ}=90^{\circ}$，即$\angle EOG = 90^{\circ}$。所以$\angle EOG$的大小和$\angle BOD$的大小没有关系。

14. 如图，点O在直线AB上，OC⊥AB，在三角形ODE中，∠ODE = 90°，∠EOD = 60°，先将三角形ODE一边OE与OC重合，然后绕点O顺时针方向旋转，当OE与OB重合时停止旋转.
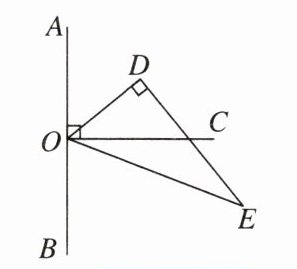
(1)当OD在OA与OC之间，且∠COD = 20°时，则∠AOE =________.
(2)试探索：在三角形ODE旋转过程中，∠AOD与∠COE大小的差是否发生变化？若不变，请求出这个差值；若变化，请说明理由.
(3)在三角形ODE旋转过程中，若∠AOE = 7∠COD，试求∠AOE的大小.

答案：
[解]
(1)$130^{\circ}$ [点拨]因为$OC\perp AB$，所以$\angle AOC = 90^{\circ}$。因为$OD$在$OA$与$OC$之间，$\angle COD = 20^{\circ}$，$\angle EOD = 60^{\circ}$，所以$\angle COE = 60^{\circ}-20^{\circ}=40^{\circ}$。所以$\angle AOE=\angle AOC+\angle COE=90^{\circ}+40^{\circ}=130^{\circ}$。
(2)在三角形$ODE$旋转过程中，$\angle AOD$与$\angle COE$的差不发生变化。有两种情况：①如图①。因为$\angle AOD+\angle COD = 90^{\circ}$，$\angle COD+\angle COE = 60^{\circ}$，所以易得$\angle AOD-\angle COE=90^{\circ}-60^{\circ}=30^{\circ}$；
　　　　　
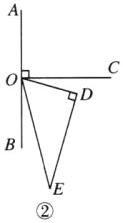
②如图②。因为$\angle AOD=\angle AOC+\angle COD = 90^{\circ}+\angle COD$，$\angle COE=\angle DOE+\angle DOC = 60^{\circ}+\angle DOC$，所以$\angle AOD-\angle COE=(90^{\circ}+\angle COD)-(60^{\circ}+\angle COD)=30^{\circ}$。综上，在三角形$ODE$旋转过程中，$\angle AOD$与$\angle COE$的差不发生变化，这个差值为$30^{\circ}$。
(3)如图①。因为$\angle AOE = 7\angle COD$，$\angle AOC = 90^{\circ}$，$\angle DOE = 60^{\circ}$，所以$90^{\circ}+60^{\circ}-\angle COD = 7\angle COD$。所以$\angle COD = 18.75^{\circ}$。所以$\angle AOE = 7\times18.75^{\circ}=131.25^{\circ}$；如图②。因为$\angle AOE = 7\angle COD$，$\angle AOC = 90^{\circ}$，$\angle DOE = 60^{\circ}$，所以$90^{\circ}+60^{\circ}+\angle COD = 7\angle COD$。所以$\angle COD = 25^{\circ}$。所以$\angle AOE = 7\times25^{\circ}=175^{\circ}$。综上，$\angle AOE = 131.25^{\circ}$或$175^{\circ}$。