《2025年综合应用创新题典中点七年级数学下册冀教版》

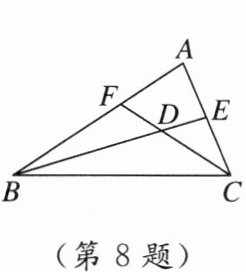
8. 如图，BE，CF都是△ABC的角平分线，且∠BDC = 130°，则∠A = （ ）

A. 50°
B. 60°
C. 70°
D. 80°

答案： D 【点拨】因为$BE$，$CF$都是$\triangle ABC$的角平分线，所以$\angle A = 180^{\circ}-(\angle ABC+\angle ACB)=180^{\circ}-2(\angle DBC+\angle BCD)$. 又因为$\angle DBC+\angle BCD = 180^{\circ}-\angle BDC$，所以$\angle A = 180^{\circ}-2(180^{\circ}-\angle BDC)=2\angle BDC - 180^{\circ}$. 又因为$\angle BDC = 130^{\circ}$，所以$\angle A = 2\times130^{\circ}-180^{\circ}=80^{\circ}$.

9. [新视角 动点探究题] 如图，∠AOB = 70°，点M，N分别在OA，OB上运动（不与点O重合），ME平分∠AMN，ME的反向延长线与∠MNO的平分线交于点F，在M，N的运动过程中，∠F的度数 （ ）

A. 变大
B. 变小
C. 等于55°
D. 等于35°

答案： D 【点拨】因为$ME$平分$\angle AMN$，$NF$平分$\angle MNO$，所以$\angle EMN=\frac{1}{2}\angle AMN$，$\angle MNF=\frac{1}{2}\angle MNO$. 因为$\angle AMN=\angle AOB+\angle MNO$，所以$\angle EMN=\frac{1}{2}\angle AOB+\angle MNF$. 又因为$\angle AOB = 70^{\circ}$，所以$\angle EMN=\frac{1}{2}\times70^{\circ}+\angle MNF = 35^{\circ}+\angle MNF$. 又因为$\angle EMN=\angle F+\angle MNF$，所以$\angle F = 35^{\circ}$.

10. [2024达州] 如图，在△ABC中，AE₁，BE₁分别是内角∠CAB，外角∠CBD的三等分线，且∠E₁AD = $\frac{1}{3}$∠CAB，∠E₁BD = $\frac{1}{3}$∠CBD，在△ABE₁中，AE₂，BE₂分别是内角∠E₁AB，外角∠E₁BD的三等分线，且∠E₂AD = $\frac{1}{3}$∠E₁AB，∠E₂BD = $\frac{1}{3}$∠E₁BD，…，以此规律作下去，若∠C = m°，则∠Eₙ = ________°.

答案： $\frac{m}{3^{n}}$【点拨】因为$\angle E_{1}AD=\frac{1}{3}\angle CAB$，$\angle E_{1}BD=\frac{1}{3}\angle CBD$，设$\angle E_{1}AD=\alpha$，$\angle E_{1}BD=\beta$，则$\angle CAB = 3\alpha$，$\angle CBD = 3\beta$. 由三角形的外角的性质得$\beta=\alpha+\angle E_{1}$，$3\beta = 3\alpha+\angle C$，所以$\angle E_{1}=\frac{1}{3}\angle C$，同理可求$\angle E_{2}=\frac{1}{3}\angle E_{1}$，所以$\angle E_{2}=(\frac{1}{3})^{2}\angle C$，$\cdots$，$\angle E_{n}=(\frac{1}{3})^{n}\angle C$，即$\angle E_{n}=(\frac{m}{3^{n}})^{\circ}$.

11. 在△ABC中，∠ACB＞∠ABC，AD平分∠BAC.
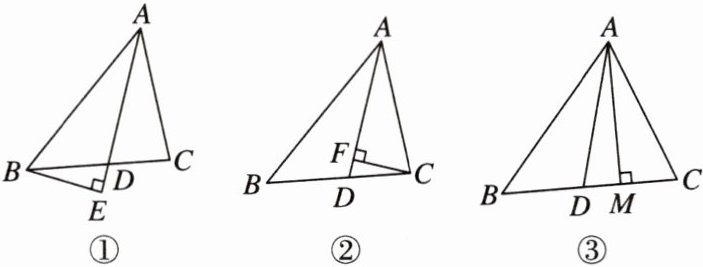
(1)如图①，过点B作BE⊥射线AD于点E，则∠ABE与$\frac{1}{2}$(∠ACB + ∠ABC)有何大小关系？请说明理由；
(2)如图②，过点C作CF⊥AD于点F，则∠DCF，∠ACB，∠ABC又有怎样的数量关系，请直接写出结论；
(3)如图③，过点A作AM⊥BC于点M，则∠DAM与∠ACB，∠ABC又有怎样的数量关系，请直接写出结论.

答案： 【解】
(1)$\angle ABE=\frac{1}{2}(\angle ACB+\angle ABC)$. 理由：在$\triangle ABE$中，因为$BE\perp$射线$AD$，所以$\angle E = 90^{\circ}$，所以$\angle ABE = 90^{\circ}-\angle BAE$. 因为$AD$平分$\angle BAC$，所以$\angle BAE=\frac{1}{2}\angle BAC$. 所以$\angle ABE = 90^{\circ}-\frac{1}{2}\angle BAC$. 又因为在$\triangle ABC$中，$\angle BAC = 180^{\circ}-\angle ACB-\angle ABC$，所以$\angle ABE = 90^{\circ}-\frac{1}{2}(180^{\circ}-\angle ACB-\angle ABC)=\frac{1}{2}(\angle ACB+\angle ABC)$.
(2)$\angle DCF=\frac{1}{2}(\angle ACB - \angle ABC)$.
(3)$\angle DAM=\frac{1}{2}(\angle ACB - \angle ABC)$.

12. [2024张家口期末] 如图，将三角形纸片ABC按如图方式折叠，折痕分别为DC和DE，点A与BC边上的点G重合，点B与DG延长线上的点F重合. 若满足∠ACB = 38°，则∠CEF = ________°.

答案： 38 【点拨】由折叠可知$\angle DCE=\angle ACD=\frac{1}{2}\angle ACB = 19^{\circ}$，$\angle CDG=\frac{1}{2}\angle ADG$，$\angle EDG=\frac{1}{2}\angle BDG$，$\angle BED=\angle FED$，又因为$\angle ADG+\angle BDG = 180^{\circ}$，所以$\angle CDG+\angle EDG=\frac{1}{2}(\angle ADG+\angle BDG)=90^{\circ}$，即$\angle EDC = 90^{\circ}$. 所以$\angle CED = 180^{\circ}-\angle CDE-\angle DCE = 71^{\circ}$，$\angle BED=\angle EDC+\angle DCE = 109^{\circ}$. 所以$\angle DEF=\angle BED = 109^{\circ}$. 所以$\angle CEF=\angle DEF-\angle CED = 38^{\circ}$.

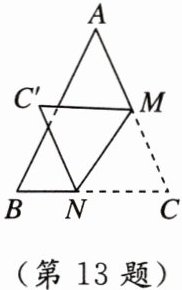
13. [新考法 分类讨论法] 如图，在△ABC中，∠B = ∠C = 65°，将△MNC沿MN折叠得△MNC'，若MC'与△ABC的边平行，则∠C'MN的度数为__________.

答案：
57.5°或25° 【点拨】分两种情况讨论：①当$C'M// BC$时，如图①，所以$\angle AMC'=\angle C = 65^{\circ}$. 所以$\angle C'MC = 180^{\circ}-\angle AMC' = 115^{\circ}$. 由折叠得$\angle C'MN=\frac{1}{2}\angle C'MC = 57.5^{\circ}$;②当$C'M// AB$时，如图②，所以$\angle C'MC=\angle A$. 因为$\angle B=\angle C = 65^{\circ}$，所以$\angle C'MC=\angle A = 180^{\circ}-2\angle B = 50^{\circ}$. 由折叠得$\angle C'MN=\frac{1}{2}\angle C'MC = 25^{\circ}$. 综上，$\angle C'MN$的度数为$57.5^{\circ}$或$25^{\circ}$.