《2025年综合应用创新题典中点七年级数学下册冀教版》

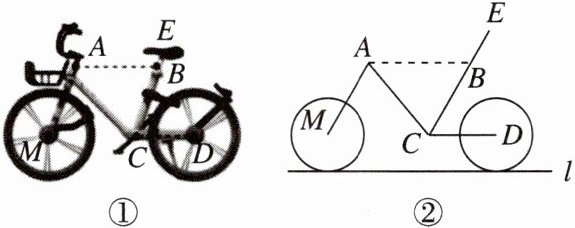
10. [情境题 实物抽象] 某市为了方便市民绿色出行，推出了共享单车服务. 图①是某品牌共享单车放在水平地面的实物图，图②是其示意图，其中AB，CD都与地面l平行，∠BCD=60°，∠BAC=50°，当∠MAC为_______度时，AM//BE.

答案： 70

11. 已知直线AB//CD，点P，Q分别在AB，CD上，如图所示，射线PB按顺时针方向以每秒5°的速度旋转至PA便立即回转，并不断往返旋转；射线QC按顺时针方向每秒1°旋转至QD停止，此时射线PB也停止旋转. 若射线QC先转60秒，射线PB才开始转动，当射线PB旋转的时间为_______秒时，PB'//QC'.

答案：
15或50或105或110　[点拨]设光线PB旋转时间为答案详解详析　　15
t秒.第一次平行时，如图①.因为PB'//QC,所以∠PB'Q=∠CQC.
　
∵AB//CD,
∴∠PB,Q=∠BPB.
∴∠CQC=∠BPB'.
∴60+t=5t.解得t=15.
　　　　 第二次平行时，如图②.因为PB//QC,所以∠CQC=
　　∠PB'C.
　
∵AB/CD,
∴∠PB'Q=∠BPB',
　
∴∠BPB'=∠CQC.
　　易得此时光线PB由PA处返回，
　
∴∠APB'=5t°−180°.
　
∴∠BPB=180°−∠APB=180°−(5t°−180°)=360°−5t°;
∴360−5t=60+t.
∴t=50;
　　第三次平行时，此时光线PB再次往PA旋转,易得
　　5t−360=60+t,解得t=105;
　　第四次平行时，此时光线PB第二次由PA处返回，易得720−5t=60+t,解得t=110.
　　故答案为15或50或105或110.

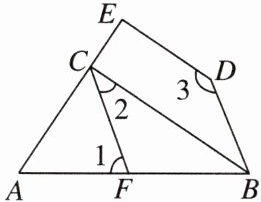
12. 如图，已知BC⊥AE，DE⊥AE，∠2+∠3=180°.
（1）请你判断CF与BD的位置关系，并说明理由；
（2）若∠1=70°，BC平分∠ABD，试求∠ACF的度数.

答案： [解]
(1)CF//DB.理由:
　
∵BC⊥AE,DE⊥AE,
∴BC//DE.
　
∴∠3+∠CBD=180°.
　
∵∠2+∠3=180°'
∴∠2=∠CBD.
∴CF//DB,
(2)
∵∠1=70°,CF//DB,
∴∠ABD=70°.
∵BC平分∠ABD,
∴∠DBC=$\frac{1}{2}$∠ABD=35°.
∴∠2=∠DBC=35°,
∵BC⊥AE,
∴∠ACB=90°.
∴∠ACF=90°−∠2=90°−35°=55°.

13. 已知直线AB//CD，直线MN分别与AB，CD交于点E，F.
（1）如图①中，若EG平分∠BEF，FG平分∠EFD，则∠G=_______°；
（2）如图②，若∠BEF=140°，FP平分∠EFD，EH平分∠BEF交CD于H，交FP于G，HP平分∠EHD，求∠P的度数.

答案：
[解]
(1)90　　[点拨]过点G作GH//AB,如图①所示.
　
∵AB//CD,
∴AB//GH//CD.
　
∴∠BEF+∠EFD=180°,∠BEG=∠EGH,∠DFG=
　　∠FGH.
　
∴∠BEG+∠DFG=∠EGH+∠FGH=∠EGF.
　
∵EG平分∠BEF,FG平分∠EFD,
　
∴∠BEG=$\frac{1}{2}$∠BEF,∠DFG=$\frac{1}{2}$∠EFD.
　
∴∠BEG+∠DFG=$\frac{1}{2}$(∠BEF+∠EFD)=90°.
　
∴∠EGF=∠BEG+∠DFG=90°.
　　　　
(2)过点P作PK//AB,如图②所示.
∵EG平分∠BEF,∠BEF=140°,
∴∠BEH=∠FEH=$\frac{1}{2}$∠BEF=70°.
∵AB//CD,PK//AB,
∴AB//PK//CD.
∴∠BEF+∠EFD=180°,∠BEH+∠EHD=180°,∠KPH=∠DHP,∠KPF=∠PFH.
∴∠EFD=180°−∠BEF=180°−140°=40°,∠EHD=
180°−∠BEH=180°−70°=110°.
∵FP平分∠EFD,HP平分∠EHD,
∴∠PFH=$\frac{1}{2}$∠EFD=20°,∠DHP=$\frac{1}{2}$∠EHD=55°.
∴∠KPH=∠DHP=55°,∠KPF=∠PFH=20°.
∴∠FPH=∠KPH−∠KPF=55°−20°=35°.