《2025年综合应用创新题典中点七年级数学下册冀教版》

1. 某班四位同学画出的线段BD，其中能表示△ABC的高的是 （ ）

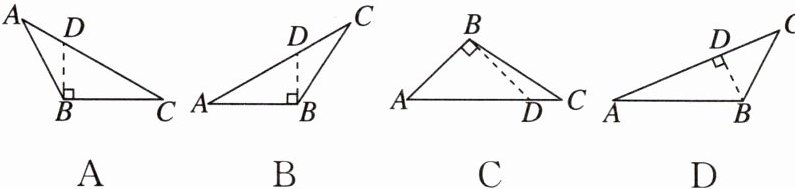
答案： D

2. 如图，在△ABC中，∠C = 90°，D，E是AC上两点，且AE = DE，BD平分∠EBC，则下列说法中不正确的是 （ ）

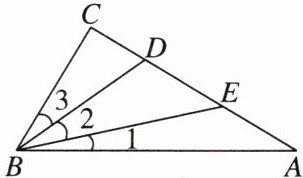
A. BE是△ABD的中线
B. BD是△BCE的角平分线
C. ∠1 = ∠2 = ∠3
D. BC是△BDE的高

答案： C

3. [2024德州] 如图，在△ABC中，AD是高，AE是中线，AD = 4，S_{△ABC}= 12，则BE的长为 （ ）

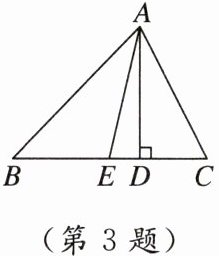
A. 1.5
B. 3
C. 4
D. 6

答案： B 【点拨】$\because S_{\triangle ABC}=\frac{1}{2}BC\cdot AD = 12$，$AD = 4$，$\therefore BC = 6$. 又$\because AE$是中线，$\therefore BE=\frac{1}{2}BC = 3$.

4. 如图，已知点D是△ABC的重心，连接AD，并延长交BC于点E，AB = 4，△ABE的周长比△ACE的周长大1.8，则AC = ________.

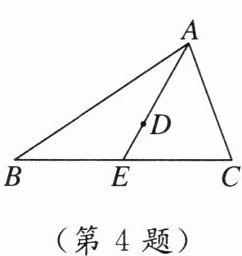
答案： 2.2 【点拨】$\because$点$D$是$\triangle ABC$的重心，且$AD$的延长线交$BC$于点$E$，$\therefore E$是$BC$的中点，即$BE = CE$.$\because\triangle ABE$的周长比$\triangle ACE$的周长大$1.8$，$\therefore AB + BE + AE-(AC + CE + AE)=1.8$，即$AB - AC = 1.8$. 又$\because AB = 4$，$\therefore AC = 4 - 1.8 = 2.2$.

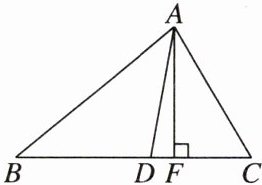
5. 如图，在△ABC中，AF是高，AD平分∠BAC，∠BAC = 80°，∠C = 60°，求∠DAF的度数.

答案： 【解】$\because AF$是$\triangle ABC$的高，
$\therefore\angle AFC = 90^{\circ}$.$\therefore\angle C+\angle CAF = 90^{\circ}$.
又$\because\angle C = 60^{\circ}$，$\therefore\angle CAF = 30^{\circ}$.
$\because AD$平分$\angle BAC$，$\angle BAC = 80^{\circ}$，
$\therefore\angle CAD = 40^{\circ}$.
$\therefore\angle DAF=\angle CAD-\angle CAF = 40^{\circ}-30^{\circ}=10^{\circ}$.

6. 如图，在△ABC中，AE是角平分线，AD是中线，AF是高，下列结论不一定成立的是（ ）

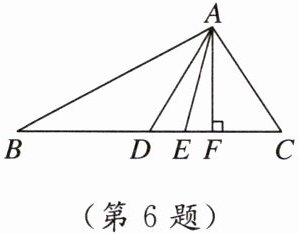
A. BC = 2CD
B. ∠BAE = $\frac{1}{2}$∠BAC
C. ∠AFB = 90°
D. AD = CD

答案： D

7. 如图，每个小正方形的边长均为1，则下列三角形（阴影部分）的面积与△ABC面积相等的是 （ ）

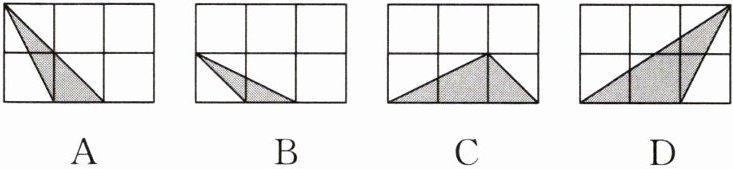
答案： A

8. [新考法 分类讨论法] 已知AD为△ABC的高，若BC = 10，BD = 4，则CD = ________.

答案：
6或14 【点拨】分两种情况讨论：①当高$AD$在$\triangle ABC$的内部时，如图①.$\because BC = 10$，$BD = 4$，$\therefore CD = BC - BD = 10 - 4 = 6$；②当高$AD$在$\triangle ABC$的外部时，如图②.$\because BC = 10$，$BD = 4$，$\therefore CD = BC + BD = 10 + 4 = 14$. 综上，$CD = 6$或14.

9. 如图，已知AM是△ABC的中线，P是AC边上一动点，若△ABC的面积为10，AC = 4，则MP的最小值为________.

答案： 2.5 【点拨】$\because AM$是$\triangle ABC$的中线，$\triangle ABC$的面积为$10$，$\therefore S_{\triangle ACM}=\frac{1}{2}S_{\triangle ABC}=5$. 易知当$MP\perp AC$时，$MP$的值最小，$\therefore S_{\triangle ACM}=\frac{1}{2}AC\cdot MP = 5$. 又$\because AC = 4$，$\therefore\frac{1}{2}\times4\times MP = 5$.$\therefore MP = 2.5$.

10. [新考法 发现规律法] 如图，在1个面积为S的等边三角形中，连接三条边中点得到4个相同的三角形，将中间的三角形涂成白色，记为第1次操作；再对其余3个三角形进行同样的操作，记为第2次操作；按照上述规律继续操作，则经过n次操作后，该等边三角形中白色三角形的面积之和是________.

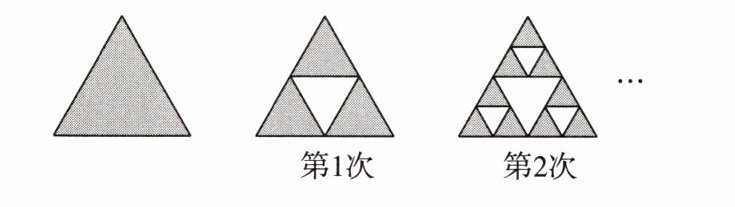
答案： $S - (\frac{3}{4})^{n}S$ 【点拨】$\because$在面积为$S$的等边三角形中，连接三条边中点得到$4$个相同的三角形，$\therefore$第$1$次操作后，黑色三角形的面积是$\frac{3}{4}S$；第$2$次操作后，黑色三角形的面积是$(\frac{3}{4})^{2}S$；第$3$次操作后，黑色三角形的面积是$(\frac{3}{4})^{3}S$，$\cdots$，第$n$次操作后，黑色三角形的面积是$(\frac{3}{4})^{n}S$，$\therefore$经过$n$次操作后，该等边三角形中白色三角形的面积之和$=S - (\frac{3}{4})^{n}S$.