《2025年综合应用创新题典中点七年级数学下册冀教版》

1. 在解方程组$\begin{cases}3x - y = 8,①\\y = x + 1②\end{cases}$的过程中，将②代入①可得 （ ）
A. $3x - x + 1 = 8$
B. $3x + 3 - x = 8$
C. $3x - x - 1 = 8$
D. $3x - x = 8$

答案： C

2. [2024石家庄长安区期末] 用代入法解二元一次方程组$\begin{cases}2x + y = 5,①\\3x + 4y = 7②\end{cases}$的过程中，下列变形不正确的是 （ ）
A. 由①得$x = \frac{5 - y}{2}$
B. 由①得$y = 5 - 2x$
C. 由②得$x = \frac{7 + 4y}{3}$
D. 由②得$y = \frac{7 - 3x}{4}$

答案： C [点拨]由①得$y = 5 - 2x$或$x=\frac{5 - y}{2}$，
故A，B正确，不符合题意；
由②得$x=\frac{7 - 4y}{3}$或$y=\frac{7 - 3x}{4}$，
故C不正确，符合题意；D正确，不符合题意.

3. [2024秦皇岛期末] 对于二元一次方程组$\begin{cases}\cdots,①\\3x - y = 8,②\end{cases}$把①代入②消去$y$后所得到的方程为$3x - x - 5 = 8$，则①可以是 （ ）
A. $y = x + 5$
B. $y = x - 5$
C. $x = 2y + 5$
D. $x = 3y - 5$

答案： A

4. [新趋势 学科内综合] 若$-3x^{m - 1}y^{3}$与$5x^{n}y^{m + n}$的和是单项式，则$m$，$n$的值分别是 （ ）
A. $m = 2$，$n = - 1$
B. $m = - 2$，$n = - 1$
C. $m = 2$，$n = 1$
D. $m = - 2$，$n = 1$

答案： C [点拨]由题意，得$\begin{cases}m - 1 = n\\m + n = 3\end{cases}$，解得$\begin{cases}m = 2\\n = 1\end{cases}$.

5. [新考法 图表信息法] 下面是小明同学解方程组$\begin{cases}2x - 8y = 13,\\4x + 2y = - 1\end{cases}$过程的框图表示，请你帮他补充完整：
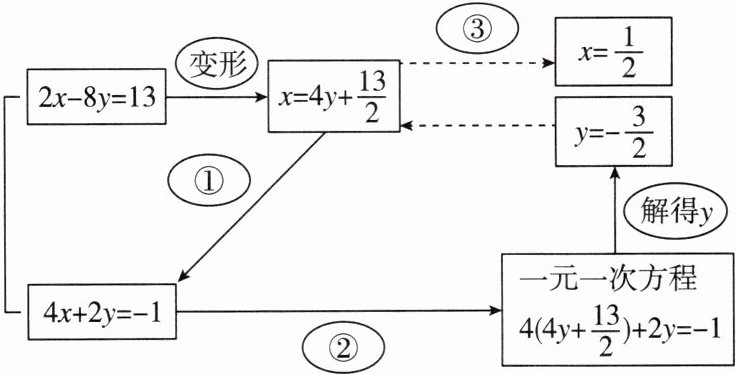
其中，①为__________，②为__________，③为__________.

答案： 代入；消去$x$；解得$x$

6. [母题 教材P8习题T2] 用代入消元法解下列方程组：
（1）$\begin{cases}2x + 3y = - 19,①\\x = 1 - 5y;②\end{cases}$
（2）[2024浙江]$\begin{cases}2x - y = 5,①\\4x + 3y = - 10.②\end{cases}$

答案： [解]
(1)把②代入①，得$2(1 - 5y)+3y = - 19$，解得$y = 3$，
把$y = 3$代入②，得$x = 1 - 5×3 = - 14$，
所以方程组的解为$\begin{cases}x = - 14\\y = 3\end{cases}$；
(2)由①，得$y = 2x - 5$，③
把③代入②，得$4x + 3(2x - 5)= - 10$，解得$x=\frac{1}{2}$，
把$x=\frac{1}{2}$代入③，得$y = 2×\frac{1}{2}-5$，解得$y = - 4$，
所以方程组的解为$\begin{cases}x=\frac{1}{2}\\y = - 4\end{cases}$.

7. 已知关于$x$，$y$的二元一次方程组$\begin{cases}kx - 3y = 14\\y = 3x - 1\end{cases}$有正整数解，则整数$k =$ （ ）
A. 9
B. 10
C. 10或20
D. 20

答案： C [点拨]$\begin{cases}kx - 3y = 14,①\\y = 3x - 1,②\end{cases}$将②代入①，得$kx - 3(3x - 1)=14$，解得$x=\frac{11}{k - 9}$. 因为$x$是正整数，所以$k - 9 = 1$或11. 所以$k = 10$或$k = 20$. 经检验，$k = 10$和$k = 20$时，$y$的值也为正整数，满足题意. 故选C.

8. [2024·上海徐汇区期末 新考法 新定义计算法] 定义一种新运算“※”，规定：$x※y = ax + by^{2}$，其中$a$，$b$为常数，且$7※2 = 11$，$2※4 = 18$，则$3※1 =$ （ ）
A. 3
B. 4
C. 5
D. 6

答案： B [点拨]因为$x※y = ax + by^{2}$，且$7※2 = 11$，$2※4 = 18$，所以$\begin{cases}7a + 4b = 11\\2a + 16b = 18\end{cases}$，解得$\begin{cases}a = 1\\b = 1\end{cases}$. 所以$x※y = x + y^{2}$.
所以$3※1 = 3 + 1^{2}=4$. 故选B.

9. 为确保信息安全，信息需加密传输，发送方由明文→密文(加密)，接收方由密文→明文(解密)，已知加密规则为：明文$a$，$b$，$c$，$d$对应密文$a + 2b$，$2b + c$，$2c + 3d$，$4d$. 例如，明文1，2，3，4对应密文5，7，18，16. 当接收方收到密文14，9，23，28时，则解密得到的明文为（ ）
A. 7，7，1，4
B. 6，4，1，7
C. 4，6，1，7
D. 1，6，4，7

答案： B [点拨]由题意可得，$a + 2b = 14$，$2b + c = 9$，$2c + 3d = 23$，$4d = 28$，解得$a = 6$，$b = 4$，$c = 1$，$d = 7$. 所以解密得到的明文为6，4，1，7.

10. 已知方程组$\begin{cases}x - 2y = - 1,\\x + 2y = n\end{cases}$和$\begin{cases}x + y = m,\\x - y = 2\end{cases}$的解相同，则$2m - n =$________.

答案： 5 [点拨]由题意得$\begin{cases}x - 2y = - 1\\x - y = 2\end{cases}$，解得$\begin{cases}x = 5\\y = 3\end{cases}$. 将$x = 5$，$y = 3$代入$x + 2y = n$，得$n = 11$，将$x = 5$，$y = 3$代入$x + y = m$，得$m = 8$，所以$2m - n = 2×8 - 11 = 5$.