第102页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
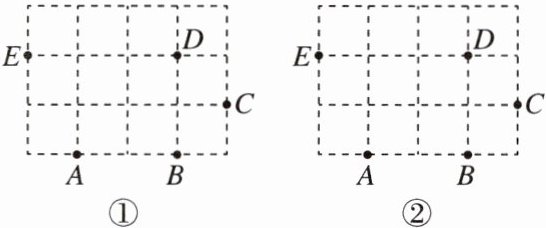
10. 如图,过A,B,C,D,E五个点中任意三点画三角形.
(1) 以AB为一边可以画出______个三角形,请在图①中画出图形;
(2) 以C为顶点可以画出______个三角形,请在图②中画出图形.
(1) 以AB为一边可以画出______个三角形,请在图①中画出图形;
(2) 以C为顶点可以画出______个三角形,请在图②中画出图形.

答案:
【解】
(1)3
画出的△ABC,△ABD,△ABE如图①所示.
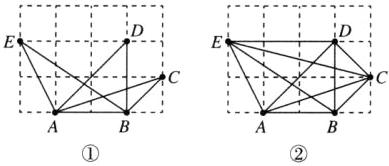
(2)6
画出的△ABC,△ACD,△ACE,△BCD,△BCE,△CDE如图②所示.
【解】
(1)3
画出的△ABC,△ABD,△ABE如图①所示.

(2)6
画出的△ABC,△ACD,△ACE,△BCD,△BCE,△CDE如图②所示.
11. 已知a,b,c为三角形的三边长,化简:|b + c - a| + |b - c - a| - |c - a - b| - |a - b + c|.
答案:
【解】
∵a,b,c为三角形的三边长,
∴a + b > c,a + c > b,b + c > a.
∴原式=|(b + c) - a| + |b - (c + a)| - |c - (a + b)| - |(a + c) - b| = b + c - a + a + c - b - a - b + c + b - a - c = 2c - 2a.
∵a,b,c为三角形的三边长,
∴a + b > c,a + c > b,b + c > a.
∴原式=|(b + c) - a| + |b - (c + a)| - |c - (a + b)| - |(a + c) - b| = b + c - a + a + c - b - a - b + c + b - a - c = 2c - 2a.
12. 新考法 分类讨论法 已知a,b,c为△ABC的三边长,且b,c满足(b - 5)² + |c - 7| = 0,a为方程|a - 3| = 2的解,求△ABC的周长.
答案:
【解】
∵(b - 5)² + |c - 7| = 0,
∴$\begin{cases}b - 5 = 0 \\ c - 7 = 0\end{cases}$,解得$\begin{cases}b = 5 \\ c = 7\end{cases}$.
∵a为方程|a - 3| = 2的解,
∴a = 5或1.
当a = 1,b = 5,c = 7时,1 + 5 < 7,
不能组成三角形,故a = 1不符合题意;
当a = 5,b = 5,c = 7时,符合三角形的三边关系.
∴△ABC的周长 = 5 + 5 + 7 = 17.
∵(b - 5)² + |c - 7| = 0,
∴$\begin{cases}b - 5 = 0 \\ c - 7 = 0\end{cases}$,解得$\begin{cases}b = 5 \\ c = 7\end{cases}$.
∵a为方程|a - 3| = 2的解,
∴a = 5或1.
当a = 1,b = 5,c = 7时,1 + 5 < 7,
不能组成三角形,故a = 1不符合题意;
当a = 5,b = 5,c = 7时,符合三角形的三边关系.
∴△ABC的周长 = 5 + 5 + 7 = 17.
13. [2024廊坊校级月考] 某建材市场上的一种钢管的长度规格及相应价格如表所示. 学校要制作一个三角形支架的宣传牌,已经购买了两根长度分别为2 m和5 m的钢管,还需要购买一根.
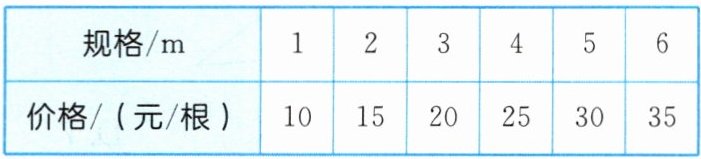
(1) 有哪几种规格的钢管可供选择?
(2) 若要求制成的三角形支架的周长为偶数,则制成一个三角形支架一共需要花多少钱购买钢管?

(1) 有哪几种规格的钢管可供选择?
(2) 若要求制成的三角形支架的周长为偶数,则制成一个三角形支架一共需要花多少钱购买钢管?
答案:
【解】
(1)设第三根钢管的长度为x m,
则5 - 2 < x < 5 + 2,即3 < x < 7,
∴长度为4 m,5 m,6 m的钢管可供选择.
(2)
∵三角形支架的周长为偶数,
∴三边长分别为2 m、5 m、5 m,
∴15×1 + 30×2 = 75(元).
答:制成一个三角形支架一共需要花75元购买钢管.
(1)设第三根钢管的长度为x m,
则5 - 2 < x < 5 + 2,即3 < x < 7,
∴长度为4 m,5 m,6 m的钢管可供选择.
(2)
∵三角形支架的周长为偶数,
∴三边长分别为2 m、5 m、5 m,
∴15×1 + 30×2 = 75(元).
答:制成一个三角形支架一共需要花75元购买钢管.
14. 新考法 从特殊到一般的思想 (1) 如图①,图中共有三角形______个;如图②,若增加一条线,则图中共有三角形______个;
(2) 如图③,若增加到10条线,请你求出图中的三角形的个数.
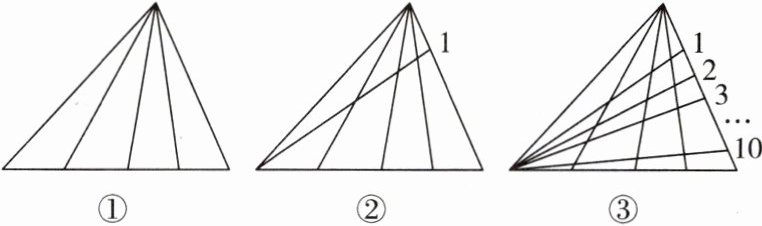
(2) 如图③,若增加到10条线,请你求出图中的三角形的个数.

答案:
【解】
(1)10;24
(2)增加1条线,三角形的个数为10 + 10×1 + 4×1;
增加2条线,三角形的个数为10 + 10×2 + 4×(2 + 1);
增加3条线,三角形的个数为10 + 10×3 + 4×(3 + 2 + 1);
…
则增加n条线,三角形的个数为10 + 10×n + 4×(n + n - 1 + n - 2 + … + 1).
所以增加10条线,三角形的个数为10 + 10×10 + 4×(10 + 9 + 8 + … + 1) = 330.
(1)10;24
(2)增加1条线,三角形的个数为10 + 10×1 + 4×1;
增加2条线,三角形的个数为10 + 10×2 + 4×(2 + 1);
增加3条线,三角形的个数为10 + 10×3 + 4×(3 + 2 + 1);
…
则增加n条线,三角形的个数为10 + 10×n + 4×(n + n - 1 + n - 2 + … + 1).
所以增加10条线,三角形的个数为10 + 10×10 + 4×(10 + 9 + 8 + … + 1) = 330.
查看更多完整答案,请扫码查看


