《2026年金考卷中考试题汇编45套数学山东专版》

22. (本小题满分11分)
已知抛物线$L: y=-x^{2}+b x+c$(b,c是常数)经过点$A(-1,1)$.
(1) 若抛物线L的对称轴为直线$x=-\frac{2}{3}$,求b,c的值.
(2) 若抛物线L还经过另一点$B(m, 1)$,且$0＜m＜1$,
①求b的取值范围;
②点$P_{1}(x_{1}, y_{1}), P_{2}(x_{2}, y_{2})$均在抛物线L上.当$x_{1}＞x_{2}$,且$x_{1}+x_{2}＞-\frac{1}{2}$时,$y_{1}＜y_{2}$,求m的最大值.

答案： 22
(1)$\because$抛物线L的对称轴为直线$x = -\frac{b}{2}$，
$\therefore -\frac{b}{2×(-1)} = -\frac{2}{3}$，解得$b = -\frac{4}{3}$ (1分)
$\because$抛物线$L:y = -x^{2} - \frac{4}{3}x + c$经过点$A(-1,1)$，
$\therefore -1 + \frac{4}{3} + c = 1$，$\therefore c = 2 - \frac{4}{3} = \frac{2}{3}$。 (3分)
(2)①方法一：$\because$抛物线L经过点$A(-1,1)$，$B(m,1)$，
$\therefore$抛物线L的对称轴为直线$x = \frac{-b}{2a} = \frac{-1 + m}{2}$
又$\because a = -1$，
$\therefore \frac{b}{2} = \frac{-1 + m}{2}$，$\therefore m = b + 1$。
$\because 0 ＜ m ＜ 1$，$\therefore 0 ＜ b + 1 ＜ 1$，
$\therefore b$的取值范围为$-1 ＜ b ＜ 0$。 (7分)
方法二：将$A(-1,1)$代入$y = -x^{2} + bx + c$，
得$-1 - b + c = 1$，$\therefore c = b + 2$，
$\therefore y = -x^{2} + bx + b + 2$。
又$\because$抛物线L过点$B(m,1)$，
$\therefore -m^{2} + bm + b + 2 = 1$，
$\therefore b(m + 1) = m^{2} - 1$。
由$0 ＜ m ＜ 1$，可知$m \neq -1$，
$\therefore b = \frac{m^{2} - 1}{m + 1} = m - 1$，
$\therefore -1 ＜ b ＜ 0$。 (7分)
②方法一：将$(-1,1)$代入$y = -x^{2} + bx + c$，
得$-1 - b + c = 1$，$\therefore c = b + 2$。
由①可知$b = m - 1$，$\therefore c = m + 1$，
$\therefore y = -x^{2} + (m - 1)x + m + 1$，
$\therefore y_{1} = -x_{1}^{2} + (m - 1)x_{1} + m + 1$，
$y_{2} = -x_{2}^{2} + (m - 1)x_{2} + m + 1$。
$\because y_{1} ＜ y_{2}$，$\therefore y_{1} - y_{2} ＜ 0$，
$\therefore -x_{1}^{2} + (m - 1)x_{1} + m + 1 + x_{2}^{2} - (m - 1)x_{2} - m - 1 = x_{2}^{2} - x_{1}^{2} + (m - 1)(x_{1} - x_{2}) ＜ 0$，
$\therefore (x_{2} - x_{1})(x_{2} + x_{1}) - (m - 1)(x_{2} - x_{1}) ＜ 0$，
$\because x_{1} ＞ x_{2}$，$\therefore x_{2} - x_{1} ＜ 0$，
$\therefore (x_{2} + x_{1}) - (m - 1) ＞ 0$，
$\therefore x_{2} + x_{1} ＞ m - 1$。 (9分)
又$\because x_{1} + x_{2} ＞ -\frac{1}{2}$，
$\therefore m - 1 \leq -\frac{1}{2}$，$\therefore m \leq \frac{1}{2}$，
$\therefore m$的最大值为$\frac{1}{2}$。 (11分)
方法二：易知抛物线L的对称轴为直线$x = \frac{b}{2}$，
则点$P_{1}(x_{1},y_{1})$到直线$x = \frac{b}{2}$的距离$d_{1} = |x_{1} - \frac{b}{2}|$，点$P_{2}(x_{2},y_{2})$到直线$x = \frac{b}{2}$的距离$d_{2} = |x_{2} - \frac{b}{2}|$。
$\because$抛物线L的开口向下，
$\therefore$距离对称轴越远的点，函数值越小，
$\therefore$当$y_{1} ＜ y_{2}$时，$d_{1} ＞ d_{2}$，
$\therefore d_{1}^{2} ＞ d_{2}^{2}$，即$(x_{1} - \frac{b}{2})^{2} ＞ (x_{2} - \frac{b}{2})^{2}$，
整理，得$x_{1}^{2} - x_{2}^{2} ＞ b(x_{1} - x_{2})$，
$\therefore (x_{1} + x_{2})(x_{1} - x_{2}) ＞ b(x_{1} - x_{2})$。
$\because x_{1} ＞ x_{2}$，$\therefore x_{1} - x_{2} ＞ 0$，
$\therefore x_{1} + x_{2} ＞ b$。 (9分)
又$\because x_{1} + x_{2} ＞ -\frac{1}{2}$，$\therefore b \leq -\frac{1}{2}$
由①可知$b = m - 1$，
$\therefore m - 1 \leq -\frac{1}{2}$，$\therefore m \leq \frac{1}{2}$，
$\therefore m$的最大值为$\frac{1}{2}$。 (11分)

23. (本小题满分11分)
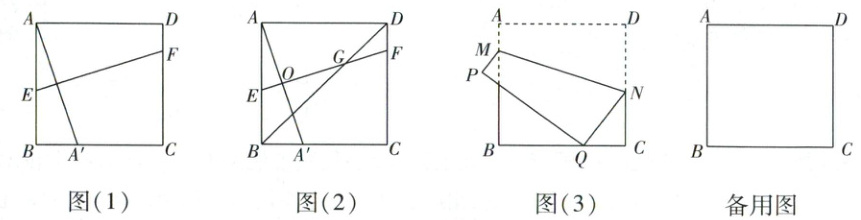
王老师善于通过合适的主题整合教学内容,帮助同学们用整体的、联系的、发展的眼光看问题,形成科学的思维习惯.下面是王老师以正方形为背景设计的问题,请你解答.
(1) 观察发现
如图(1),将正方形ABCD折叠,使点A的对应点$A'$落在BC边上,折痕分别与AB,CD交于点E,F,则折痕EF和$AA'$的数量和位置关系分别是AA' = EF，AA' \perp EF.
(2) 类比探究
在(1)的条件下,设EF与$AA'$交于点O,连接BD交EF于点G,如图(2),求证:$O G=O E+G F$.
(3) 拓展应用
如图(3),正方形ABCD的边长为$\frac{9}{2}$,点M是AB边上的一动点,点N是CD边上的一点,且$C N=2$,连接MN,将正方形ABCD沿MN折叠,使点A,D分别落在点P,Q处,当点Q落在直线BC上时,请直接写出线段AM的长.

答案：
23
(1)$AA' = EF$，$AA' \perp EF$ (2分)
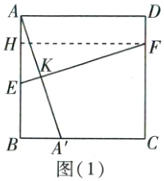
解法提示：如图
(1)，过点F作$FH \perp AB$于点H。设EF与$AA'$交于点K。
$\because \angle BAD = \angle D = \angle AHF = 90^{\circ}$，
$\therefore$四边形$AHFD$是矩形，$\therefore HF = AD$。
$\because$四边形ABCD是正方形，
$\therefore AD = AB$，$\therefore HF = AB$。
$\because EF$垂直平分$AA'$，$\therefore AA' \perp EF$，
$\therefore \angle AEK + \angle EAK = 90^{\circ}$。
又$\because \angle AEK + \angle HFE = 90^{\circ}$，
$\therefore \angle EAK = \angle HFE$。
又$\because \angle ABA' = \angle FHE = 90^{\circ}$，
$\therefore \triangle ABA' \cong \triangle FHE(ASA)$(提示：“十”字全等模型)，
$\therefore AA' = EF$。


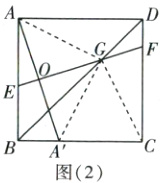
(2)证明：如图
(2)，连接AG、$GA'$、GC。
$\because BA = BC$，$\angle ABG = \angle CBG$，$BG = BG$，
$\therefore \triangle ABG \cong \triangle CBG(SAS)$， (5分)
$\therefore GA = GC$，$\angle GCB = \angle GAB$。
$\because EF$垂直平分$AA'$，$\therefore GA = GA'$，
$\therefore GA' = GC$，$\therefore \angle GA'C = \angle GCA'$，
$\therefore \angle GA'C = \angle GAB$。
又$\because \angle GA'C + \angle GA'B = 180^{\circ}$，
$\therefore \angle GA'B + \angle GAB = 180^{\circ}$，
$\therefore$在四边形$ABA'G$中，$\angle ABA' + \angle AGA' = 180^{\circ}$。
又$\because \angle ABA' = 90^{\circ}$，$\therefore \angle AGA' = 90^{\circ}$。
又$\because OA = OA'$，$\therefore OG = \frac{1}{2}AA'$，$\therefore OG = \frac{1}{2}EF$。
$\because EF = OE + GF + OG$，
$\therefore OG = OE + GF$。 (9分)
(3)线段AM的长为1或4。 (11分)
解法提示：连接MQ，设$AM = x$。
$\because AB = BC = CD = AD = \frac{9}{2}$，$CN = 2$，$\therefore BM = \frac{9}{2} - x$，$DN = \frac{5}{2}$，
$\therefore QN = DN = \frac{5}{2}$
分两种情况讨论。
①当点Q在线段BC上时，如图
(3)。
在$Rt\triangle NQC$中，$QC = \sqrt{QN^{2} - CN^{2}} = \frac{3}{2}$，
$\therefore BQ = BC - QC = \frac{9}{2} - \frac{3}{2} = 3$，
$\therefore$在$Rt\triangle BQM$中，$MQ^{2} = BM^{2} + BQ^{2} = (\frac{9}{2} - x)^{2} + 3^{2}$。
又$\because$在$Rt\triangle MPQ$中，$MQ^{2} = MP^{2} + PQ^{2} = x^{2} + (\frac{9}{2})^{2}$，
$\therefore (\frac{9}{2} - x)^{2} + 3^{2} = x^{2} + (\frac{9}{2})^{2}$，
$\therefore x = 1$。

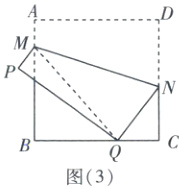
②当点Q在BC的延长线上时，如图
(4)。
在$Rt\triangle NQC$中，$QC = \sqrt{QN^{2} - CN^{2}} = \frac{3}{2}$，
$\therefore BQ = BC + QC = \frac{9}{2} + \frac{3}{2} = 6$，
$\therefore$在$Rt\triangle BQM$中，$MQ^{2} = BM^{2} + BQ^{2} = (\frac{9}{2} - x)^{2} + 6^{2}$。
又$\because$在$Rt\triangle MPQ$中，$MQ^{2} = MP^{2} + PQ^{2} = x^{2} + (\frac{9}{2})^{2}$，
$\therefore (\frac{9}{2} - x)^{2} + 6^{2} = x^{2} + (\frac{9}{2})^{2}$，$\therefore x = 4$。
综上所述，线段AM的长为1或4。