2026年金考卷中考试题汇编45套数学山东专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年金考卷中考试题汇编45套数学山东专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
8. 我们把两组邻边分别相等的四边形称之为“筝形”. 如图,在四边形 $ ABCD $中,对角线 $ AC $,$ BD $交于点 $ O $. 下列条件中,不能判断四边形 $ ABCD $是筝形的是(
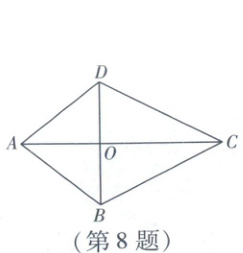
A.$ BO = DO $,$ AC\perp BD $
B.$ \angle DAC=\angle BAC $,$ AD = AB $
C.$ \angle DAC=\angle BAC $,$ \angle DCA=\angle BCA $
D.$ \angle ADC=\angle ABC $,$ BO = DO $
D
)
A.$ BO = DO $,$ AC\perp BD $
B.$ \angle DAC=\angle BAC $,$ AD = AB $
C.$ \angle DAC=\angle BAC $,$ \angle DCA=\angle BCA $
D.$ \angle ADC=\angle ABC $,$ BO = DO $
答案:
8 D 逐项分析如下,故选D.
选项 分析 正误
∵ BO=DO, AC⊥BD,
∴ AC是线段BD的垂
A 直平分线,
∴ AB=AD, BC=DC (依据:线段垂直平分线上的点到线段两端的距离相等),
∴ 四边形ABCD是筝形. √
∵ AD=AB, ∠DAC=∠BAC, AC=AC,
B
∴ △ADC ≌ △ABC,
∴ CD=CB,
∴ 四边形ABCD是筝形. √
∵ ∠DAC=∠BAC, AC=AC, ∠DCA=
C ∠BCA,
∴ △ADC ≌ △ABC,
∴ AD=AB, CD=CB,
∴ 四边形ABCD是筝形. √
由∠ADC=∠ABC, BO=DO不能判断AB=
D AD, CB=CD, 故不能判断四边形ABCD是筝形. ×
选项 分析 正误
∵ BO=DO, AC⊥BD,
∴ AC是线段BD的垂
A 直平分线,
∴ AB=AD, BC=DC (依据:线段垂直平分线上的点到线段两端的距离相等),
∴ 四边形ABCD是筝形. √
∵ AD=AB, ∠DAC=∠BAC, AC=AC,
B
∴ △ADC ≌ △ABC,
∴ CD=CB,
∴ 四边形ABCD是筝形. √
∵ ∠DAC=∠BAC, AC=AC, ∠DCA=
C ∠BCA,
∴ △ADC ≌ △ABC,
∴ AD=AB, CD=CB,
∴ 四边形ABCD是筝形. √
由∠ADC=∠ABC, BO=DO不能判断AB=
D AD, CB=CD, 故不能判断四边形ABCD是筝形. ×
9. 某广场计划用如图(1)所示的 $ A $,$ B $两种瓷砖铺成如图(2)所示的图案. 第一行第一列瓷砖的位置记为 $ (1,1) $,其右边瓷砖的位置记为 $ (2,1) $,其上面瓷砖的位置记为 $ (1,2) $,按照这样的规律,下列说法正确的是(
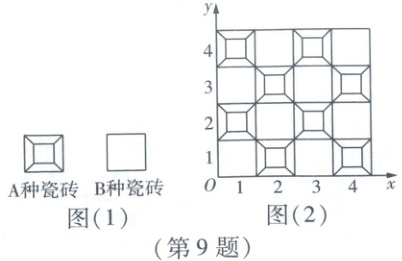
A.$ (2024,2025) $位置是 $ B $种瓷砖
B.$ (2025,2025) $位置是 $ B $种瓷砖
C.$ (2026,2026) $位置是 $ A $种瓷砖
D.$ (2025,2026) $位置是 $ B $种瓷砖
B
)
A.$ (2024,2025) $位置是 $ B $种瓷砖
B.$ (2025,2025) $位置是 $ B $种瓷砖
C.$ (2026,2026) $位置是 $ A $种瓷砖
D.$ (2025,2026) $位置是 $ B $种瓷砖
答案:
9 B 由题图
(2)可知,A种瓷砖的位置:(1,2),(1,4),(1,6),…,(2,1),(2,3),(2,5),...,B种瓷砖的位置:(1,1),(1,3),(1,5),...,(2,2),(2,4),(2,6),....由此可得,A种瓷砖的坐标规律为(奇数,偶数),(偶数,奇数),B种瓷砖的坐标规律为(奇数,奇数),(偶数,偶数),
∴ (2024,2025)位置是A种瓷砖,(2025,2025)位置是B种瓷砖,(2026,2026)位置是B种瓷砖,(2025,2026)位置是A种瓷砖.故选B.
(2)可知,A种瓷砖的位置:(1,2),(1,4),(1,6),…,(2,1),(2,3),(2,5),...,B种瓷砖的位置:(1,1),(1,3),(1,5),...,(2,2),(2,4),(2,6),....由此可得,A种瓷砖的坐标规律为(奇数,偶数),(偶数,奇数),B种瓷砖的坐标规律为(奇数,奇数),(偶数,偶数),
∴ (2024,2025)位置是A种瓷砖,(2025,2025)位置是B种瓷砖,(2026,2026)位置是B种瓷砖,(2025,2026)位置是A种瓷砖.故选B.
10. 新素材 “三进制”逻辑的芯片 2025年5月,基于“三进制”逻辑的芯片研制成功. 与传统的“二进制”芯片相比,三进制逻辑芯片在特定的运算中具有更高的效率.
二进制数的组成数字为 $ 0 $,$ 1 $. 十进制数 $ 22 $化为二进制数:
$ 22=1×2^{4}+0×2^{3}+1×2^{2}+1×2^{1}+0×2^{0}=10110_{2} $.
传统三进制数的组成数字为 $ 0 $,$ 1 $,$ 2 $. 十进制数 $ 22 $化为三进制数:
$ 22=2×3^{2}+1×3^{1}+1×3^{0}=211_{3} $.
将二进制数 $ 1011_{2} $化为三进制数为(
A.$ 102_{3} $
B.$ 101_{3} $
C.$ 110_{3} $
D.$ 12_{3} $
二进制数的组成数字为 $ 0 $,$ 1 $. 十进制数 $ 22 $化为二进制数:
$ 22=1×2^{4}+0×2^{3}+1×2^{2}+1×2^{1}+0×2^{0}=10110_{2} $.
传统三进制数的组成数字为 $ 0 $,$ 1 $,$ 2 $. 十进制数 $ 22 $化为三进制数:
$ 22=2×3^{2}+1×3^{1}+1×3^{0}=211_{3} $.
将二进制数 $ 1011_{2} $化为三进制数为(
A
)A.$ 102_{3} $
B.$ 101_{3} $
C.$ 110_{3} $
D.$ 12_{3} $
答案:
10 A
名师教解题
第一步:将二进制数$1011_2$化为十进制数
∵ 二进制数$1011_2$的各位权值从右到左依次为$2^0$, $2^1$, $2^2$, $2^3$,
∴ 其对应十进制数为$1 × 2^3 + 0 × 2^2 + 1 × 2^1 + 1 × 2^0 = 8 + 0 + 2 + 1 = 11_{10}$.
第二步:将十进制数化为三进制数
采用“除3取余法”:$11 ÷ 3 = 3 ·s 2$; $3 ÷ 3 = 1 ·s 0$; $1 ÷ 3 = 0 ·s 1$.
将余数倒序排列, 得到三进制数为$102_3$. 故选A.
名师教解题
第一步:将二进制数$1011_2$化为十进制数
∵ 二进制数$1011_2$的各位权值从右到左依次为$2^0$, $2^1$, $2^2$, $2^3$,
∴ 其对应十进制数为$1 × 2^3 + 0 × 2^2 + 1 × 2^1 + 1 × 2^0 = 8 + 0 + 2 + 1 = 11_{10}$.
第二步:将十进制数化为三进制数
采用“除3取余法”:$11 ÷ 3 = 3 ·s 2$; $3 ÷ 3 = 1 ·s 0$; $1 ÷ 3 = 0 ·s 1$.
将余数倒序排列, 得到三进制数为$102_3$. 故选A.
11. 计算:$ (\frac{1}{2})^{-1}-\sqrt{8}-(1-\sqrt[3]{2})^{0}= $
$1 - 2\sqrt{2}$
.
答案:
11 $1 - 2\sqrt{2}$
12. 若 $ 2x - 3y = 2 $,则 $ 6y - 4x + 1 = $
-3
.
答案:
12 -3
13. 一个不透明的袋子中装有 $ 2 $个绿球、$ 1 $个白球,每个球除颜色外都相同. 小明同学从袋中随机摸出 $ 1 $个球(不放回)后,小华同学再从袋中随机摸出 $ 1 $个球. 两人摸到不同颜色球的概率是
$\frac{2}{3}$
.
答案:
13 $\frac{2}{3}$
[解析]画树状图如图所示,由树状图可知,共有6种等可能的结果,其中两人摸到不同颜色球的结果有4种,故所求概率为$\frac{4}{6} = \frac{2}{3}$.

13 $\frac{2}{3}$
[解析]画树状图如图所示,由树状图可知,共有6种等可能的结果,其中两人摸到不同颜色球的结果有4种,故所求概率为$\frac{4}{6} = \frac{2}{3}$.

14. 如图,小明同学将正方形硬纸板沿实线剪开,得到一个立方体的表面展开图. 若正方形硬纸板的边长为 $ 12 $cm,则折成立方体的棱长为
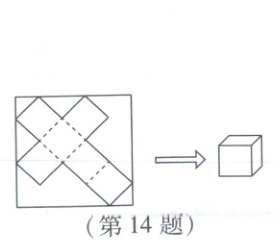
$\frac{12\sqrt{2}}{5}$
cm.
答案:
14 $\frac{12\sqrt{2}}{5}$
名师教解题
设折成立方体的棱长为$a cm$. 将已知信息和设元后得到的信息标注在如下图中.

易知∠BDC = ∠ADE = 45°,
∴ $BD = \frac{\sqrt{2}}{2}CD = 2\sqrt{2}a$, $AD = \frac{\sqrt{2}}{2}DE = \frac{\sqrt{2}}{2}a$.
∵ AD + BD = 12,
∴ $\frac{\sqrt{2}}{2}a + 2\sqrt{2}a = 12$, 解得$a = \frac{12\sqrt{2}}{5}$. 故折成立方体的棱长为$\frac{12\sqrt{2}}{5} cm$.
14 $\frac{12\sqrt{2}}{5}$
名师教解题
设折成立方体的棱长为$a cm$. 将已知信息和设元后得到的信息标注在如下图中.

易知∠BDC = ∠ADE = 45°,
∴ $BD = \frac{\sqrt{2}}{2}CD = 2\sqrt{2}a$, $AD = \frac{\sqrt{2}}{2}DE = \frac{\sqrt{2}}{2}a$.
∵ AD + BD = 12,
∴ $\frac{\sqrt{2}}{2}a + 2\sqrt{2}a = 12$, 解得$a = \frac{12\sqrt{2}}{5}$. 故折成立方体的棱长为$\frac{12\sqrt{2}}{5} cm$.
15. 如图,点 $ A $在反比例函数 $ y=\frac{4}{x} $的图象上,点 $ B $在反比例函数 $ y=-\frac{2}{x} $的图象上,连接 $ OA $,$ OB $,$ AB $. 若 $ AO\perp BO $,则 $ \tan\angle BAO = $
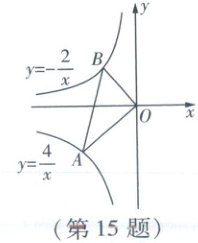
$\frac{\sqrt{2}}{2}$
.
答案:
15 $\frac{\sqrt{2}}{2}$
[解析]如图,过点A,B分别作AC⊥y轴,BD⊥y轴,垂足分别为C,D.易证△DBO ∽ △COA (点拨:“一线三直角”相似模型),
∴ $\frac{S_{△DBO}}{S_{△COA}} = (\frac{OB}{OA})^2$ (依据:相似三角形面积比等于相似比的平方).
∵ 点A在反比例函数$y = \frac{4}{x}$的图象上,点B在反比例函数$y = -\frac{2}{x}$的图象上,
∴ $S_{△BOD} = \frac{1}{2} × | -2 | = 1$, $S_{△AOC} = \frac{1}{2} × 4 = 2$ (点拨:结合反比例函数中|k|的几何意义),
∴ $\frac{1}{2} = (\frac{OB}{OA})^2$,
∴ $\frac{OB}{OA} = \frac{\sqrt{2}}{2}$,
∴ $\tan \angle BAO = \frac{OB}{OA} = \frac{\sqrt{2}}{2}$.

15 $\frac{\sqrt{2}}{2}$
[解析]如图,过点A,B分别作AC⊥y轴,BD⊥y轴,垂足分别为C,D.易证△DBO ∽ △COA (点拨:“一线三直角”相似模型),
∴ $\frac{S_{△DBO}}{S_{△COA}} = (\frac{OB}{OA})^2$ (依据:相似三角形面积比等于相似比的平方).
∵ 点A在反比例函数$y = \frac{4}{x}$的图象上,点B在反比例函数$y = -\frac{2}{x}$的图象上,
∴ $S_{△BOD} = \frac{1}{2} × | -2 | = 1$, $S_{△AOC} = \frac{1}{2} × 4 = 2$ (点拨:结合反比例函数中|k|的几何意义),
∴ $\frac{1}{2} = (\frac{OB}{OA})^2$,
∴ $\frac{OB}{OA} = \frac{\sqrt{2}}{2}$,
∴ $\tan \angle BAO = \frac{OB}{OA} = \frac{\sqrt{2}}{2}$.

查看更多完整答案,请扫码查看


