《2026年金考卷中考试题汇编45套数学山东专版》

7. 新课标 数学文化(2025兰州)《九章算术》是中国传统数学最重要的数学著作之一."方程章"第11题大意是:两匹马一头牛总价超过1万,超过部分等于半匹马的价格;一匹马两头牛的总价不足1万,不足部分等于半头牛的价格,问一匹马、一头牛的价格分别是多少?若设一匹马价格为$x$,一头牛价格为$y$,则可列方程组为

A.$\begin{cases}2x + y - 10000=\frac{1}{2}x,\\10000 - (x + 2y)=\frac{1}{2}y\end{cases}$
B.$\begin{cases}10000 - (2x + y)=\frac{1}{2}x,\\x + 2y - 10000=\frac{1}{2}y\end{cases}$
C.$\begin{cases}x + 2y - 10000=\frac{1}{2}x,\\10000 - (2x + y)=\frac{1}{2}y\end{cases}$
D.$\begin{cases}2x + y=\frac{1}{2}x,\\x + 2y=\frac{1}{2}y\end{cases}$

答案： 7 A

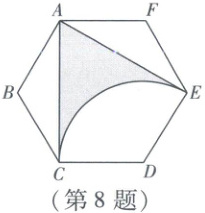
8. (2025资阳改编)如图,在正六边形$ABCDEF$中,$AB = 2$,连接$AC$,$AE$,以点$D$为圆心、$CD$的长为半径作圆弧$CE$,则图中阴影部分的面积是

A.$4\sqrt{3}+\frac{4\pi}{3}$
B.$4\sqrt{3}-\frac{4\pi}{3}$
C.$\frac{8\pi}{3}-4\sqrt{3}$
D.$4\sqrt{2}-\frac{4\pi}{3}$

答案：
8 B 如图,连接AD.
∵六边形ABCDEF为正六边形，
∴∠B = ∠BCD = ∠CDE = 120°,BC = CD = DE = AB = 2,S△ACD = S△AED,
∴∠BCA = 30°,∠CDA = ∠EDA = 60°,
∴∠ACD = 90°,
∴AC = √3CD = 2√3,
∴S阴影部分 = 2S△ACD - S扇形CDE = 2×$\frac{1}{2}$×2×2√3 - $\frac{120\pi×2²}{360}$ = 4√3 - $\frac{4\pi}{3}$.

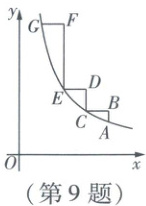
9. (2025广西)如图,在平面直角坐标系中,"双曲线阶梯"$ABCDEFG$的所有线段均与$x$轴平行或垂直,且满足$BC = DE = FG = 1$,点$A$,$C$,$E$,$G$均在双曲线$y=\frac{k}{x}$的一支上.若点$A$的坐标为$(4,\frac{3}{2})$,则第三级阶梯的高$EF$=

A.4
B.3
C.$\frac{7}{2}$
D.$\frac{5}{2}$

答案： 9 B 名师教解题
结合题干，将所得信息标注在图中：
由点$A(4,\frac{3}{2})$可知，$k = 4×\frac{3}{2}=6,\therefore y=\frac{6}{x}(x＞0)$.结合图中标注的信息可知$x_E = 2,x_C = 1,\therefore y_E=\frac{6}{2}=3,y_C=\frac{6}{1}=6,\therefore EF=y_C - y_E = 3$.

10. 从地面竖直向上抛出一小球,小球的高度$h$(单位:$m$)与小球的运动时间$t$(单位:$s$)之间的关系式是$h = 30t - 5t^{2}(0\leqslant t\leqslant6)$.有下列结论:①小球从抛出到落地需要6s;②小球运动中的高度可以是30m;③小球运动2s时的高度小于运动5s时的高度.其中,正确结论的个数是

A.0
B.1
C.2
D.3

答案： 10 C 对于$h = 30t - 5t²(0\leq t\leq6)$，令$h = 0$，则$30t - 5t² = 0$，解得$t_1 = 0,t_2 = 6,\therefore$小球从抛出到落地需要6s，故①正确.
$\because h = 30t - 5t² = -5(t - 3)² + 45,\therefore$小球运动的最大高度为45m,$\therefore$小球运动中的高度可以是30m，故②正确.对于$h = 30t - 5t²(0\leq t\leq6)$，当$t = 2$时，$h = 30×2 - 5×2² = 40$，当$t = 5$时，$h = 30×5 - 5×5² = 25,\therefore$小球运动2s时的高度大于运动5s时的高度，故③错误.故选C.

11. 新课标 开放性试题(2025广西)写出一个使分式$\frac{1}{x + 3}$有意义的$x$的值,可以是0(答案不唯一，满足$x\neq -3$即可).

答案： 11 0(答案不唯一，满足$x\neq -3$即可)

12. (2025湖南改编)在平面直角坐标系中,将点$P(-3,2)$向右平移3个单位长度到点$P_{1}$处,则点$P_{1}$的坐标为$(0,2)$.

答案： 12 $(0,2)$

13. (2025甘肃改编)关于$x$的一元二次方程$3x^{2}-6x + m = 0$有两个实数根,则$m$的取值范围是$m\leq3$.

答案： 13 $m\leq3$ [解析]$\because$方程$3x² - 6x + m = 0$有两个实数根，$\therefore \Delta = (-6)² - 4×3m\geq0$，解得$m\leq3$.

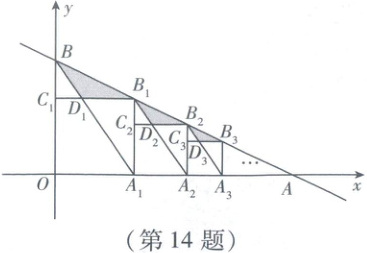
14. (2025龙东地区)如图,在平面直角坐标系中,直线$y = -\frac{1}{2}x + 3$交$x$轴于点$A$,交$y$轴于点$B$.四边形$OA_{1}B_{1}C_{1}$,$A_{1}A_{2}B_{2}C_{2}$,$A_{2}A_{3}B_{3}C_{3}$,…都是正方形,顶点$A_{1}$,$A_{2}$,$A_{3}$,…都在$x$轴上,顶点$B_{1}$,$B_{2}$,$B_{3}$,…都在直线$y = -\frac{1}{2}x + 3$上,连接$BA_{1}$,$B_{1}A_{2}$,$B_{2}A_{3}$,…,分别交$C_{1}B_{1}$,$C_{2}B_{2}$,$C_{3}B_{3}$,…于点$D_{1}$,$D_{2}$,$D_{3}$,…设$\triangle BB_{1}D_{1}$,$\triangle B_{1}B_{2}D_{2}$,$\triangle B_{2}B_{3}D_{3}$,…的面积分别为$S_{1}$,$S_{2}$,$S_{3}$,…,则$S_{2025}$=$(\frac{2}{3})^{4049}$.

答案： 14 $(\frac{2}{3})^{4049}$ [解析]易知$OA = 6,OB = 3,A_1B_1 = B_1C_1 = 2,\therefore BC_1 = 1,\therefore S_{\triangle BB_1C_1} = 1$.易证$\triangle BC_1D_1\backsim\triangle A_1B_1D_1,\therefore\frac{C_1D_1}{D_1B_1}=\frac{BC_1}{B_1A_1}=\frac{BC_1}{B_1C_1}=\frac{1}{2},\therefore S = S_{\triangle BB_1D_1}=\frac{2}{3}S_{\triangle BB_1C_1}=\frac{2}{3}$.同理可求$S_2 = S_{\triangle B_1B_1D_1}=(\frac{2}{3})^3,S_3 = S_{\triangle B_2B_3D_2}=(\frac{2}{3})^5·s·s$故$S_n = (\frac{2}{3})^{2n - 1},\therefore S_{2025}=(\frac{2}{3})^{4049}$.