2026年金考卷中考试题汇编45套数学山东专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年金考卷中考试题汇编45套数学山东专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第119页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
20. (本小题满分10分)
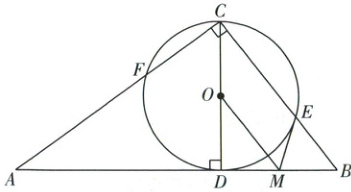
(2025南充)如图,$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CD\perp AB$于点$D$,以$CD$为直径的$\odot O$交$BC$于点$E$,交$AC$于点$F$,$M$为线段$DB$上一点,$ME = MD$,连接$OM$.
(1)求证:$ME$是$\odot O$的切线.
(2)若$CF = 3$,$\sin B=\frac{4}{5}$,求$OM$的长.
(2025南充)如图,$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CD\perp AB$于点$D$,以$CD$为直径的$\odot O$交$BC$于点$E$,交$AC$于点$F$,$M$为线段$DB$上一点,$ME = MD$,连接$OM$.
(1)求证:$ME$是$\odot O$的切线.
(2)若$CF = 3$,$\sin B=\frac{4}{5}$,求$OM$的长.

答案:
20
(1)证明:如图,连接OE.
$\because CD\perp AB,\therefore \angle ODM = 90°$. (1分)
在$\triangle ODM$与$\triangle OEM$中,$OD = OE,OM = OM,DM = EM,\therefore \triangle ODM\cong\triangle OEM(SSS)$ (3分)
$\therefore \angle OEM = \angle ODM = 90°,\therefore ME$为$\odot O$的切线. (5分)

(2)如图,连接DF. (6分)
$\because \angle ACB = 90°,CD\perp AB,\therefore \angle A + \angle B = \angle A + \angle ACD = 90°,\therefore \angle B = \angle ACD,\therefore \sin\angle ACD = \sin B = \frac{4}{5}$. (7分)
$\because CD$为$\odot O$的直径,$\therefore \angle CFD = 90°,\therefore \sin\angle ACD = \frac{DF}{CD}=\frac{4}{5}$.
设$DF = 4x,CD = 5x$,
在$Rt\triangle CDF$中,根据勾股定理得$CD² = DF² + CF²$,
$\therefore (5x)² = (4x)² + 3²,\therefore x = 1$(负值已舍去),$\therefore CD = 5,\therefore OD = \frac{5}{2}$.
$\because \triangle ODM\cong\triangle OEM,\therefore \angle1 = \angle2$.
$\because \angle1 + \angle2 = \angle3 + \angle4,\angle3 = \angle4$,
$\therefore \angle1 = \angle3,\therefore OM// CB$,
$\therefore \sin\angle OMD = \sin B = \frac{4}{5}\therefore OM = \frac{OD}{\sin\angle OMD}=\frac{25}{8}$. (10分)
20
(1)证明:如图,连接OE.
$\because CD\perp AB,\therefore \angle ODM = 90°$. (1分)
在$\triangle ODM$与$\triangle OEM$中,$OD = OE,OM = OM,DM = EM,\therefore \triangle ODM\cong\triangle OEM(SSS)$ (3分)
$\therefore \angle OEM = \angle ODM = 90°,\therefore ME$为$\odot O$的切线. (5分)

(2)如图,连接DF. (6分)
$\because \angle ACB = 90°,CD\perp AB,\therefore \angle A + \angle B = \angle A + \angle ACD = 90°,\therefore \angle B = \angle ACD,\therefore \sin\angle ACD = \sin B = \frac{4}{5}$. (7分)
$\because CD$为$\odot O$的直径,$\therefore \angle CFD = 90°,\therefore \sin\angle ACD = \frac{DF}{CD}=\frac{4}{5}$.
设$DF = 4x,CD = 5x$,
在$Rt\triangle CDF$中,根据勾股定理得$CD² = DF² + CF²$,
$\therefore (5x)² = (4x)² + 3²,\therefore x = 1$(负值已舍去),$\therefore CD = 5,\therefore OD = \frac{5}{2}$.
$\because \triangle ODM\cong\triangle OEM,\therefore \angle1 = \angle2$.
$\because \angle1 + \angle2 = \angle3 + \angle4,\angle3 = \angle4$,
$\therefore \angle1 = \angle3,\therefore OM// CB$,
$\therefore \sin\angle OMD = \sin B = \frac{4}{5}\therefore OM = \frac{OD}{\sin\angle OMD}=\frac{25}{8}$. (10分)
21. (本小题满分9分)
(2025山西)项目学习
项目背景:
如图(1),"源池泉涌"为我省某景区的一个景点,主体设计包括外栏墙与内栏墙,外栏墙高于内栏墙,两栏中间为步道,内栏墙内为泉池,池内泉水清澈见底.从正上方看,外栏墙呈正八边形,内栏墙呈圆形.综合实践小组的同学围绕"景物的测量与计算"开展项目学习活动,形成了如下活动报告.
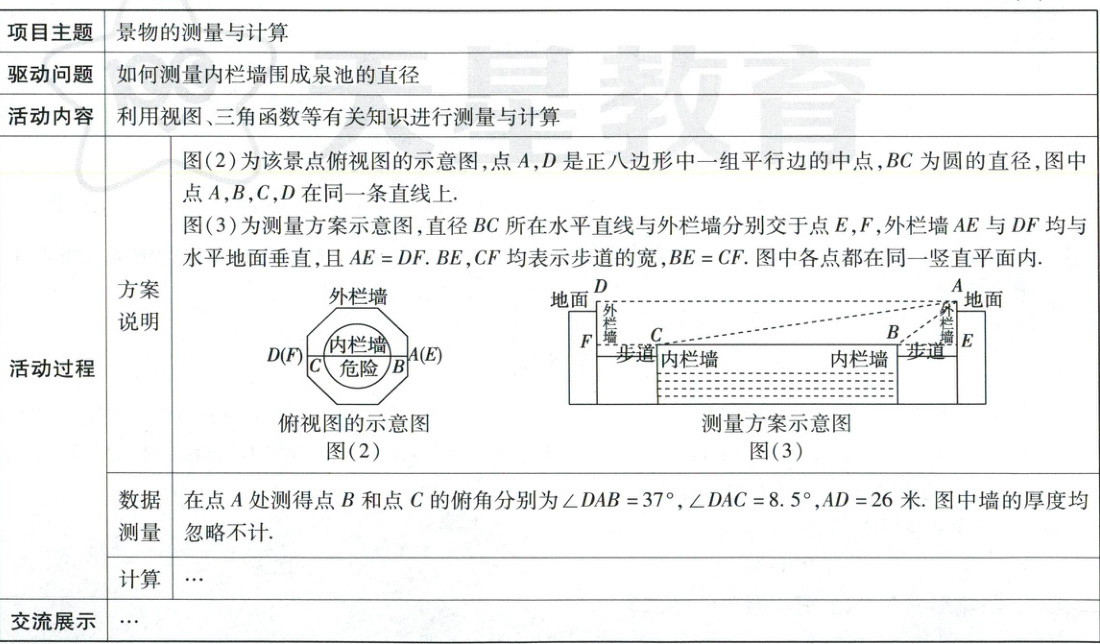
请根据上述数据,计算内栏墙围成泉池的直径$BC$的长(结果精确到1米.参考数据:$\sin8.5^{\circ}\approx0.15$,$\cos8.5^{\circ}\approx0.99$,$\tan8.5^{\circ}\approx0.15$,$\sin37^{\circ}\approx0.60$,$\cos37^{\circ}\approx0.80$,$\tan37^{\circ}\approx0.75$).
(2025山西)项目学习
项目背景:
如图(1),"源池泉涌"为我省某景区的一个景点,主体设计包括外栏墙与内栏墙,外栏墙高于内栏墙,两栏中间为步道,内栏墙内为泉池,池内泉水清澈见底.从正上方看,外栏墙呈正八边形,内栏墙呈圆形.综合实践小组的同学围绕"景物的测量与计算"开展项目学习活动,形成了如下活动报告.


请根据上述数据,计算内栏墙围成泉池的直径$BC$的长(结果精确到1米.参考数据:$\sin8.5^{\circ}\approx0.15$,$\cos8.5^{\circ}\approx0.99$,$\tan8.5^{\circ}\approx0.15$,$\sin37^{\circ}\approx0.60$,$\cos37^{\circ}\approx0.80$,$\tan37^{\circ}\approx0.75$).
答案:
21 由题意得,$\angle AEF = 90°$,四边形AEFD为矩形, (1分)
$\therefore EF = AD = 26$米,$AD// EF$,
$\therefore \angle ABE = \angle DAB = 37°,\angle ACE = \angle DAC = 8.5°$. (3分)
设$BE = CF = x$米,则$CE = (26 - x)$米,$BC = (26 - 2x)$米.在$Rt\triangle ABE$中,$\angle AEB = 90°,\tan\angle ABE = \frac{AE}{BE}$,
$\therefore AE = BE·\tan\angle ABE = x·\tan37°$. (5分)
在$Rt\triangle ACE$中,$\angle AEC = 90°,\tan\angle ACE = \frac{AE}{CE}$,
$\therefore AE = CE·\tan\angle ACE = (26 - x)·\tan8.5°$,
$\therefore x·\tan37° = (26 - x)·\tan8.5°$. (7分)
解得$x\approx\frac{13}{3}$,
$\therefore BC = 26 - 2×\frac{13}{3}\approx17$(米).
答:内栏墙围成泉池的直径BC的长约为17米. (9分)
$\therefore EF = AD = 26$米,$AD// EF$,
$\therefore \angle ABE = \angle DAB = 37°,\angle ACE = \angle DAC = 8.5°$. (3分)
设$BE = CF = x$米,则$CE = (26 - x)$米,$BC = (26 - 2x)$米.在$Rt\triangle ABE$中,$\angle AEB = 90°,\tan\angle ABE = \frac{AE}{BE}$,
$\therefore AE = BE·\tan\angle ABE = x·\tan37°$. (5分)
在$Rt\triangle ACE$中,$\angle AEC = 90°,\tan\angle ACE = \frac{AE}{CE}$,
$\therefore AE = CE·\tan\angle ACE = (26 - x)·\tan8.5°$,
$\therefore x·\tan37° = (26 - x)·\tan8.5°$. (7分)
解得$x\approx\frac{13}{3}$,
$\therefore BC = 26 - 2×\frac{13}{3}\approx17$(米).
答:内栏墙围成泉池的直径BC的长约为17米. (9分)
查看更多完整答案,请扫码查看


