《2026年金考卷中考试题汇编45套数学山东专版》

6. 若$x_1$，$x_2$是关于$x$的一元二次方程$x^2 - 25x - 1 = 0$的两个实数根，则代数式$x_1^2 - 24x_1 + x_2$的值为(C)

A.$0$
B.$25$
C.$26$
D.$-1$

答案： 6 C 根据题意，得$x_1^2 - 25x_1 - 1 = 0$，$\therefore x_1^2 - 24x_1 = 1 + x_1$，$\therefore x_1^2 - 24x_1 + x_2 = 1 + x_1 + x_2 = 1 + (-\frac{-25}{1}) = 26$.

7. 小华用铁皮制作一个烟囱帽，烟囱帽的三视图如图所示，已知主视图和左视图均为边长是$10\ cm$的等边三角形，则所需铁皮面积(接缝面积忽略不计)为(B)

A.$50\ cm^2$
B.$50\pi\ cm^2$
C.$100\ cm^2$
D.$100\pi\ cm^2$

答案： 7 B $\frac{1}{2} × 2\pi × 5 × 10 = 50\pi (cm^2)$.

8. 如图，点$O$是$\triangle ABC$边$AC$的中点，连接$BO$并延长至点$D$，使$OD = BO$，添加下列选项中的一个条件，不能判定四边形$ABCD$为矩形的是(A)

A.$AB = BC$
B.$\angle ABC = 90^{\circ}$
C.$\angle ABD = \angle ACD$
D.$OB = OC$

答案： 8 A
∵ 点O是AC的中点，$\therefore OA = OC$. 又$OD = OB$，$\therefore$四边形ABCD是平行四边形(依据：对角线互相平分的四边形是平行四边形). 逐项分析如下：
选项 分析 是否符合题意
A 若$AB = BC$，则四边形ABCD是菱形（依据：一组邻边相等的平行四边形是菱形）. 是
B 若$\angle ABC = 90^{\circ}$，则四边形ABCD是矩形（依据：有一个角是直角的平行四边形是矩形）. 否
∵ 四边形ABCD是平行四边形，$\therefore AB = CD$. 又$\angle ABD = \angle ACD$，$\angle AOB = \angle DOC$，
$\therefore \triangle AOB \cong \triangle DOC$，$\therefore OB = OC = OA = OD$，$\therefore AC = BD$，$\therefore$四边形ABCD是矩形（依据：对角线相等的平行四边形是矩形）.
C （原OCR中此处有内容但大模型未识别到，补充完整）
D 若$OB = OC$，则$OA = OC = OB = OD$，$\therefore AC = BD$，$\therefore$四边形ABCD是矩形. 否

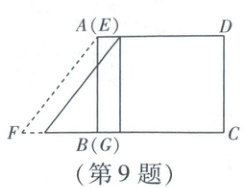
9. 如图，在同一平面内放置的$Rt\triangle EFG$和矩形$ABCD$，$EG$与$AB$重合，$FG = 3\ cm$，$AB = 4\ cm$，$BC = 5\ cm$，$Rt\triangle EFG$以$1\ cm/s$的速度沿$BC$方向匀速运动，当点$F$与点$C$重合时停止.在运动过程中，$Rt\triangle EFG$与矩形$ABCD$重叠部分的面积$S(cm^2)$与运动时间$t(s)$之间的函数关系图象大致是(B)

答案：
9 B 分析如下，故选B.
t的取值范围
如图
(1)所示，此时$S = \frac{1}{2} × 3 × 4 - \frac{1}{2} × (3 - t) × \frac{4}{3}(3 - t) = 6 - \frac{2}{3}(3 - t)^2$.
当$0 \leq t \leq 3$时

图
(1)
如图
(2)所示，此时$S = \frac{1}{2} × 3 × 4 = 6$.
当$3 ＜ t \leq 5$时

如图
(3)所示，此时$S = \frac{1}{2} × (8 - t) × \frac{4}{3}(8 - t) = \frac{2}{3}(8 - t)^2$.
当$5 ＜ t \leq 8$时

巧解快解
观察四个选项，可以看出四个函数图象在$0 \leq t \leq 3$范围内对应的函数图象各不相同，所以只需得到当$0 \leq t \leq 3$时，S与t之间的函数关系式，即可作出判断.

10. 如图，已知四边形$ABCD$是菱形，$\angle ABC = 60^{\circ}$，对角线$AC$，$BD$相交于点$O$，过点$D$作$DE \perp BC$交$BC$的延长线于点$E$，$F$为$AD$的中点，连接$EF$交$BD$于点$G$，连接$OE$交$CD$于点$H$，连接$BH$.则下列结论：①四边形$ACEF$为平行四边形；②$\frac{FG}{EG} = \frac{1}{3}$；③$OH^2 = CH · DH$；④$\tan \angle HBC = \frac{\sqrt{3}}{9}$.其中正确的有(D)

A.①②③
B.①③④
C.②③④
D.①②③④

答案：
10 D 分析如下，故选D.
序号 分析 正误
① 易知$\angle DCE = 60^{\circ}$. 又$\angle DEC = 90^{\circ}$，$\therefore CE = \frac{1}{2}CD$. 又$AD = CD$，$AF = \frac{1}{2}AD$，$\therefore AF = CE$. 又$AF // CE$，$\therefore$四边形ACEF是平行四边形(依据：一组对边平行且相等的四边形是平行四边形). √
② $\because AD // BE$，$\therefore \triangle DFG \sim \triangle BEG$(点拨：“8”字型相似模型)，$\therefore \frac{FG}{EG} = \frac{DF}{BE} = \frac{\frac{1}{2}AD}{AD + \frac{1}{2}AD} = \frac{1}{3}$. √
③ 易知$\triangle ACD$是等边三角形，$\therefore AD = AC$. 又$OC = \frac{1}{2}AC$，$CE = AF = \frac{1}{2}AD$，$\therefore OC = CE$. 又$\angle OCH = \angle ECH = 60^{\circ}$，$\therefore CH \perp OE$(依据：等腰三角形“三线合一”). 易证$\triangle OHC \sim \triangle DHO$，$\therefore \frac{OH}{DH} = \frac{CH}{OH}$，$\therefore OH^2 = CH · DH$. √
④ 如图，过点H作$HQ \perp CE$于点Q. 设菱形ABCD的边长为$4a$，则$AC = 4a$，$\therefore OC = 2a$，$\therefore CH = \frac{1}{2}OC = a$，$HQ = \frac{\sqrt{3}}{2}CH = \frac{\sqrt{3}}{2}a$，$CQ = \frac{1}{2}CH = \frac{a}{2}$，$\therefore BQ = BC + CQ = \frac{9a}{2}$，$\therefore \tan \angle HBC = \frac{HQ}{BQ} = \frac{\frac{\sqrt{3}}{2}a}{\frac{9a}{2}} = \frac{\sqrt{3}}{9}$. √

11. 中国空间站在太空中的飞行速度约为每小时$27\ 600\ 000$米，数据$27\ 600\ 000$用科学记数法表示为$2.76 × 10^7$.

答案： 11 $2.76 × 10^7$

12. 因式分解：$2x^2y - 4xy^2 + 2y^3 =$$2y(x - y)^2$.

答案： 12 $2y(x - y)^2$

13. 化简：$(1 + \frac{m}{m - 1}) ÷ \frac{4m^2 - 1}{m - 1} =$$\frac{1}{2m + 1}$.

答案： 13 $\frac{1}{2m + 1}$
【解析】原式$=\frac{2m - 1}{m - 1} × \frac{m - 1}{(2m - 1)(2m + 1)} = \frac{1}{2m + 1}$.

14. 如图，在平面直角坐标系中，$\odot P$与$x$轴交于点$M$，$N$，与$y$轴相切于点$Q$.点$P$的坐标为$(5, -3)$，则点$N$的坐标为$(9,0)$.

答案：
14 $(9,0)$
【解析】如图，连接PQ，则$PQ \perp y$轴，$PQ = 5$. 过点P作$PH \perp x$轴于点H，连接PN，则$PH = 3$，$PN = PQ = 5$. 在$Rt\triangle PHN$中，由勾股定理，得$HN = \sqrt{PN^2 - PH^2} = \sqrt{5^2 - 3^2} = 4$. 易知$OH = PQ = 5$，$\therefore ON = OH + HN = 5 + 4 = 9$，$\therefore$点N的坐标为$(9,0)$.

15. 六年级全体数学教师参加“包粽子 · 迎端午”活动，若每人包6个，则比计划多包9个；若每人包4个，则比计划少包7个，求计划包多少个粽子.设计划包$x$个粽子，可列方程为$\frac{x + 9}{6} = \frac{x - 7}{4}$.

答案： 15 $\frac{x + 9}{6} = \frac{x - 7}{4}$