《2026年金考卷中考试题汇编45套数学山东专版》

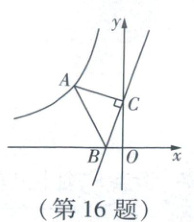
16. 如图，一次函数$y = 3x + 3$的图象与坐标轴分别交于点$B$，$C$，反比例函数$y = \frac{k}{x}(x ＜ 0)$的图象经过点$A$，$\triangle ABC$是等腰直角三角形，$\angle ACB = 90^{\circ}$，$AC = BC$，则$k$的值为-12.

答案：
16 -12
【解析】易得$B(-1,0)$，$C(0,3)$，$\therefore OB = 1$，$OC = 3$. 如图，过点A作$AD \perp y$轴于点D. 易证$\triangle ADC \cong \triangle COB$(点拨：“一线三直角”全等模型)，$\therefore AD = CO = 3$，$CD = OB = 1$，$\therefore OD = 4$，$\therefore A(-3,4)$，$\therefore k = -3 × 4 = -12$.

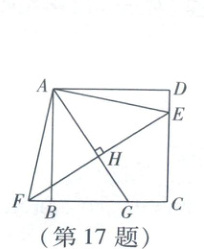
17. 如图，四边形$ABCD$是正方形，$E$为$CD$上一点，将$\triangle ADE$绕点$A$顺时针旋转$90^{\circ}$至$\triangle ABF$，连接$EF$，$AH \perp EF$于点$H$，交$BC$于点$G$，若$BG = 2$，$CG = 1$，则$CE$的长为$\frac{12}{5}$.

答案：
17 $\frac{12}{5}$
【解析】如图，连接EG. 易知G,B,F三点共线. 由旋转的性质可得$DE = BF$，$AE = AF$. 又$AH \perp EF$，$\therefore EH = FH$(依据：等腰三角形“三线合一”)，$\therefore AH$垂直平分EF，$\therefore EG = FG$(依据：线段垂直平分线上的点到线段两端点的距离相等). 易知$CD = BC = 3$. 设$CE = x$，则$BF = DE = 3 - x$，$\therefore EG = FG = 5 - x$. 在$Rt\triangle CEG$中，由勾股定理，得$EG^2 = CE^2 + CG^2$，即$(5 - x)^2 = x^2 + 1$，解得$x = \frac{12}{5}$，即$CE = \frac{12}{5}$.

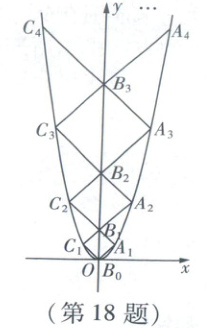
18. 二次函数$y = x^2$的图象如图所示，点$B_0$位于坐标原点，点$B_1$，$B_2$，$·s$，$B_n$在$y$轴的正半轴上，点$A_1$，$A_2$，$·s$，$A_n$，点$C_1$，$C_2$，$·s$，$C_n$在二次函数的图象上，四边形$B_0A_1B_1C_1$，四边形$B_1A_2B_2C_2$，$·s$，四边形$B_{n - 1}A_nB_nC_n$都是正方形，则正方形$B_{n - 1}A_nB_nC_n$的周长为$4\sqrt{2}n$.

答案： 18 $4\sqrt{2}n$
【解析】设点$A_1(m,m^2)$，易知$m = m^2$，整理得$m(m - 1) = 0$，解得$m_1 = 0$(舍去)，$m_2 = 1$，$\therefore A_1(1,1)$，$\therefore B_0A_1 = \sqrt{2}$，$\therefore$正方形$B_0A_1B_1C_1$的周长为$4\sqrt{2}$. 易得$B_1(0,2)$. 设点$A_2(t,t^2)$，则$t = t^2 - 2$，解得$t_1 = -1$(舍去)，$t_2 = 2$，$\therefore A_2(2,4)$，$\therefore B_1A_2 = 2\sqrt{2}$，$\therefore$正方形$B_1A_2B_2C_2$的周长为$8\sqrt{2}$. 同理可得，正方形$B_2A_3B_3C_3$的周长为$12\sqrt{2}·s ·s$故正方形$B_{n - 1}A_nB_nC_n$的周长为$4\sqrt{2}n$.

19. （本题满分8分）
（1）计算：$(\frac{1}{2})^{-1} - \sqrt[3]{8} + |1 - \sqrt{3}| + (2 - \sqrt{3}\tan 60^{\circ})^{2025}$；
（2）解不等式组$\begin{cases}x + 3 ＞ -2x, \\ 2x - 5 \leq 1,\end{cases}$并把它的解集表示在如图所示的数轴上.

答案： 19
(1)原式$= 2 - 2 + \sqrt{3} - 1 + (2 - 3)^{2025}$ (2分)
$= \sqrt{3} - 1 - 1$
$= \sqrt{3} - 2$. (4分)
(2)$\begin{cases} x + 3 ＞ -2x, & ① \\ 2x - 5 \leq 1. & ② \end{cases}$
解不等式①，得$x ＞ -1$； (5分)
解不等式②，得$x \leq 3$， (6分)
所以不等式组的解集为$-1 ＜ x \leq 3$.
不等式组的解集在数轴上表示如图所示：
不等式组的解集在数轴上表示如图所示： -4 -3 -2 -1 0 1 2 3 4
(8分)

20. (本题满分8分)
东营市各县区积极创建全国义务教育城乡优质均衡发展县，为了解城乡教育质量发展情况，从农村和城区各抽取1所学校进行艺术抽测，每个学校均随机抽测了10名学生，数据分析如下.
(一)收集与整理
农村学校10名学生的艺术成绩(单位：分).
64，74，78，82，84，86，86，92，96，98；
城区学校10名学生的艺术成绩(单位：分).
62，70，79，83，85，87，87，90，97，100.
(二)描述与分析
城乡学生艺术成绩的平均数、中位数、众数和方差如下：

根据以上信息，回答下列问题：
(1)$a =$85，$b =$87，$c =$95.2；
(三)迁移与应用
(2)若从本次艺术成绩在95分以上的4名学生中，任意选择2名学生参加艺术展演，请用列表法或画树状图的方法求出所选2名学生恰好都是城区学生的概率；
(3)请从以上统计量中，任选一个统计量，对这2所学校的艺术成绩进行对比分析，并对艺术教学提出一条合理化建议.

答案：
20
(1)85 87 95.2 (3分)
(2)农村学校95分以上学生有2人，分别记为$A_1$，$A_2$，城区学校95分以上学生有2人，分别记为$B_1$，$B_2$，画树状图如下：

由树状图可知，共有12种可能的结果，每种结果出现的可能性相同，其中所选2名学生恰好都是城区学生的结果有2种，
$\therefore P(所选2名学生恰好都是城区学生) = \frac{2}{12} = \frac{1}{6}$. (6分)
(3)答案不唯一，只要能对平均数、中位数、众数、方差任一统计量进行比较，数据大小比较正确，建议合理即给满分.
例：从平均数看，城区学校和农村学校的艺术成绩水平相同，建议继续保持城乡优质均衡发展；
从中位数看，城区学校的艺术成绩的中位数高于农村学校的艺术成绩的中位数，建议加强农村学校艺术教学；
从众数看，城区学校的艺术成绩的众数高于农村学校的艺术成绩的众数，建议提高农村学校艺术教学水平；
从方差看，城区学校艺术成绩的方差大于农村学校艺术成绩的方差，城区学校艺术成绩波动较大，建议减小两极分化.