《2026年金考卷中考试题汇编45套数学山东专版》

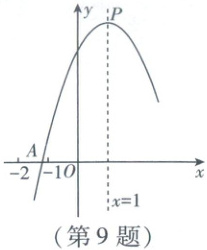
9. 如图，二次函数$y=ax^{2}+bx+c$的部分图象与$x$轴的一个交点A位于$(-2,0)$和$(-1,0)$之间，顶点P的坐标为$(1,n)$. 下列结论：①$abc＜0$；②对于任意实数$m$，都有$am^{2}+bm-a-b＞0$；③$3b＜2c$；④若该二次函数的图象与$x$轴的另一个交点为B，且$\triangle PAB$是等边三角形，则$n=-\frac{3}{a}$. 其中所有正确结论的序号是(D)

A.①②
B.①③
C.①④
D.①③④

答案： 9 D 逐个分析如下. 故选 D.
结论 分析 正误
$\because$ 抛物线开口向下, $\therefore a ＜ 0$. 又 $\because - \frac{b}{2a} = 1$, $\therefore b ＞ 0$. $\because$ 抛物线与 $y$ 轴交于正半轴, $\therefore c ＞ 0$, $\therefore abc ＜ 0$. $\surd$
对于 $y = ax^{2} + bx + c$, 当 $x = 1$ 时, $y_{max} = a + b + c$, $\therefore$ 对于任意实数 $m$, 都有 $am^{2} + bm + c \leq a + b + c$, 即 $am^{2} + bm - a - b \leq 0$. $×$
观察函数图象, 当 $x = -1$ 时, $y = a - b + c ＞ 0$①. $\because - \frac{b}{2a} = 1$, $\therefore - \frac{b}{2} = a$②, 将②代入①, 得 $- \frac{b}{2} - b + c ＞ 0$, 整理得 $2c ＞ 3b$. $\surd$
易得 $A(1 - \frac{\sqrt{3}}{3}n, 0)$, $B(1 + \frac{\sqrt{3}}{3}n, 0)$ (点拨: 利用三角函数求得). 根据根与系数的关系可得 $(1 - \frac{\sqrt{3}}{3}n)(1 + \frac{\sqrt{3}}{3}n) = \frac{c}{a}$①. $\because$ 抛物线的顶点坐标为 $(1, n)$, $\therefore a + b + c = n$②, 将 $b = -2a$ 代入②, 整理得 $c = n + a$③, 将③代入①, 整理得 $1 - \frac{n^{2}}{3} = \frac{n}{a} + 1$, $\therefore n = - \frac{3}{a}$. $\surd$

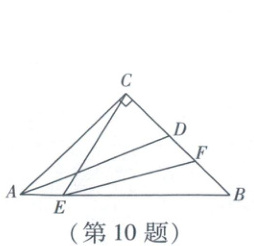
10. 如图，在$\triangle ABC$中，$\angle ACB=90^{\circ}$，$AC=BC$，AD是角平分线. 点E从点A出发，沿AB方向向点B运动，连接CE，点F在BC上，且$\angle CEF=45^{\circ}$. 设$AE=x$，$FD=y$，若$y$关于$x$的函数图象过点$(0,2-\sqrt{2})$，则该图象上最低点的坐标为(B)

A.$(\frac{1}{2},\frac{3}{2}-\sqrt{2})$
B.$(\frac{\sqrt{2}}{2},\frac{3}{2}-\sqrt{2})$
C.$(\frac{1}{2},3-2\sqrt{2})$
D.$(\frac{\sqrt{2}}{2},3-2\sqrt{2})$

答案：
10 B 由 $y$ 关于 $x$ 的函数图象过点 $(0, 2 - \sqrt{2})$ 可知, 点 $E$ 与点 $A$ 重合时, $FD = 2 - \sqrt{2}$, 即 $BD = 2 - \sqrt{2}$. 如图, 过点 $D$ 作 $DG \perp AB$ 于点 $G$. $\because AD$ 是 $\angle CAB$ 的平分线, $CD \perp AC$, $\therefore CD = GD = \frac{\sqrt{2}}{2}BD = \sqrt{2} - 1$ (依据: 角平分线上的点到角两边的距离相等), $\therefore BC = CD + BD = 1$, $\therefore AB = \sqrt{2}BC = \sqrt{2}$. 易证 $\triangle ACE \sim \triangle BEF$ (点拨: “一线三等角” 相似模型), $\therefore \frac{AE}{BF} = \frac{AC}{BE}$, 即 $\frac{x}{(2 - \sqrt{2}) - y} = \frac{1}{\sqrt{2} - x}$, 整理得 $y = x^{2} - \sqrt{2}x + 2 - \sqrt{2} = (x - \frac{\sqrt{2}}{2})^{2} + \frac{3}{2} - \sqrt{2}$, $\therefore$ 函数图象的最低点的坐标为 $(\frac{\sqrt{2}}{2}, \frac{3}{2} - \sqrt{2})$.

11. 2025年2月2日是第29个“世界湿地日”，主题是“保护湿地共筑未来”. 国家林草局公布的最新数据显示，全国湿地面积稳定保持在56 350 000公顷以上. 将数据56 350 000用科学记数法表示为$5.635 × 10^{7}$.

答案： 11 $5.635 × 10^{7}$

12. 实数$3\sqrt{2}$的整数部分为4.

答案： 12 4

13. 因式分解：$2x^{2}-12xy+18y^{2}=$$2(x - 3y)^{2}$.

答案： 13 $2(x - 3y)^{2}$

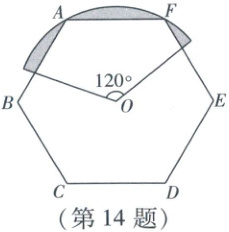
14. 如图，正六边形ABCDEF的边长为4，中心为点O，以点O为圆心，AB长为半径作圆心角为$120^{\circ}$的扇形，则图中阴影部分的面积为$\frac{16\pi}{3} - 8\sqrt{3}$.

答案：
14 $\frac{16\pi}{3} - 8\sqrt{3}$
快招解题法 试题秒解 考场速用
第一步: 选定使用的方法 (整体作差 + 等面积转化), 作辅助线如图, 连接 $OA$, $OB$, $OF$.
第二步: 求涉及的扇形的半径、圆心角, 并将面积转化易知 $\triangle ABO$, $\triangle AOF$ 均是等边三角形, $\therefore AO = BO = 4$, $\angle AOB = \angle AOF = 60^{\circ}$, $\therefore \angle BOF = 120^{\circ}$, $\therefore \angle BON + \angle NOF = 120^{\circ}$. 又 $\because \angle FOM + \angle NOF = 120^{\circ}$, $\therefore \angle BON = \angle FOM$. 又 $\because OB = OF$, $\angle NBO = \angle MFO = 60^{\circ}$, $\therefore \triangle BON \cong \triangle FOM$, $\therefore S_{\triangle BON} = S_{\triangle FOM}$, $\therefore S_{五边形ANOMF} = S_{四边形ABOF}$,
第三步: 求阴影部分的面积
$\therefore S_{阴影} = S_{扇形POQ} - S_{四边形ABOF} = \frac{120\pi · 4^{2}}{360} - 4 × 2\sqrt{3} = \frac{16\pi}{3} - 8\sqrt{3}$.

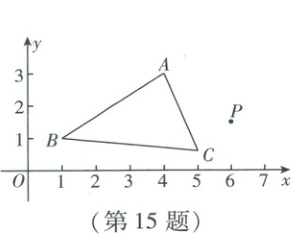
15. 如图，在平面直角坐标系中，点P的坐标为$(6,\frac{3}{2})$，$\triangle ABC$的顶点A的坐标为$(4,3)$. 以点P为位似中心作$\triangle A_{1}B_{1}C_{1}$与$\triangle ABC$位似，相似比为2，且与$\triangle ABC$位于点P同侧；以点P为位似中心作$\triangle A_{2}B_{2}C_{2}$与$\triangle A_{1}B_{1}C_{1}$位似，相似比为2，且与$\triangle A_{1}B_{1}C_{1}$位于点P同侧……按照以上规律作图，点$A_{3}$的坐标为$(-10, \frac{27}{2})$.

答案： 15 $(-10, \frac{27}{2})$
【解析】根据题意可知 $A_{1}P = 2AP$, $A_{2}P = 2A_{1}P$, $A_{3}P = 2A_{2}P ·s ·s$ 易得 $AP = \sqrt{(6 - 4)^{2} + (\frac{3}{2} - 3)^{2}} = \frac{5}{2}$, $\therefore A_{1}P = 2AP = 5$, $A_{2}P = 2A_{1}P = 10$, $A_{3}P = 2A_{2}P = 20$. 易知点 $A$, $A_{1}$, $A_{2}$, $A_{3}$, $·s$ 在直线 $AP$ 上. 设直线 $AP$ 的解析式为 $y = kx + b (k \neq 0)$, 将 $A(4, 3)$, $P(6, \frac{3}{2})$ 分别代入, 得 $\begin{cases}3 = 4k + b, \\ \frac{3}{2} = 6k + b,\end{cases}$ 解得 $\begin{cases}k = - \frac{3}{4}, \\ b = 6.\end{cases}$ $\therefore y = - \frac{3}{4}x + 6$. 设 $A_{3}(m, - \frac{3}{4}m + 6)$, $\therefore (m - 6)^{2} + (- \frac{3}{4}m + 6 - \frac{3}{2})^{2} = 20^{2}$, 解得 $m_{1} = -10$, $m_{2} = 22$ (舍去), $\therefore A_{3}(-10, \frac{27}{2})$.

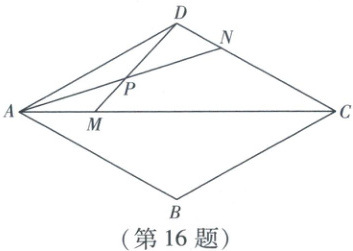
16. 如图，在菱形ABCD中，$\angle BAD=60^{\circ}$，对角线$AC=6cm$. 点M从点A出发，沿AC方向以$1cm/s$的速度向点C运动，同时，点N从点C出发，沿CD方向以$\sqrt{3}cm/s$的速度向点D运动，当一点到达终点时，另一点随之停止运动，连接AN，DM交于点P. 在此过程中，点P的运动路径长为$\frac{2\sqrt{3}\pi}{3}$cm.

答案：
16 $\frac{2\sqrt{3}\pi}{3}$
【解析】由题意可知 $\frac{AM}{CN} = \frac{1}{\sqrt{3}}$. 如图, 过点 $D$ 作 $DE \perp AC$ 于点 $E$, 则 $AE = EC = \frac{1}{2}AC = 3$ (cm) (依据: 等腰三角形 “三线合一”), $\therefore AD = \frac{AE}{\cos 30^{\circ}} = 2\sqrt{3}$ (cm), $\therefore \frac{AM}{CN} = \frac{AD}{AC} = \frac{2\sqrt{3}}{6} = \frac{\sqrt{3}}{3}$, $\therefore \frac{AM}{CN} = \frac{AD}{AC}$
又 $\because \angle DAM = \angle ACN = 30^{\circ}$, $\therefore \triangle DAM \sim \triangle ACN$,
$\therefore \angle NAC = \angle MDA$. $\because \angle APM = \angle PAD + \angle MDA = \angle PAD + \angle NAC = \angle DAM = 30^{\circ}$, $\therefore \angle APD = 150^{\circ}$, $\therefore$ 点 $P$ 在 $\triangle APD$ 的外接圆上, 设其圆心为点 $O$, 如图所示, 在优弧 $AD$ 上任取点 $Q$, 连接 $AQ$, $DQ$, $OA$, $OD$, 则 $\angle Q = 180^{\circ} - \angle APD = 30^{\circ}$ (依据: 圆内接四边形对角互补), $\because OA = OD$, $\therefore \angle AOD = 2\angle Q = 60^{\circ}$ (依据: 圆周角定理), $\therefore \triangle OAD$ 是等边三角形, $\therefore OA = AD = 2\sqrt{3}$ cm, 由题意知 $CD = AD = 2\sqrt{3}$ cm, 点 $N$ 从点 $C$ 运动到点 $D$ 所需时间为 $2\sqrt{3} ÷ \sqrt{3} = 2$ (s), 点 $M$ 从点 $A$ 运动到点 $C$ 需时间为 $6 ÷ 1 = 6$ (s), $\therefore$ 点 $N$ 到达点 $D$ 时, 两点同时停止运动, 此时点 $P$ 与点 $D$ 重合, $\therefore$ 点 $P$ 的运动路径是 $\overset{\frown}{AD}$, $\therefore$ 点 $P$ 的运动路径长为 $\frac{60\pi · 2\sqrt{3}}{180} = \frac{2\sqrt{3}\pi}{3}$ (cm).

名师辨模型
动点问题中常见的隐形圆模型
类型 动点到定点的距离为定值 定弦对定角
说明及图示 若 $AB$ 为定线段, $C$ 为平面内一点, 且 $\angle ACB = \alpha$, 则点 $C$ 在以 $AB$ 为弦的定圆上. 当 $\alpha = 90^{\circ}$ 时, 点 $C$ 在以 $AB$ 为直径的圆上. 当 $\alpha ＜ 90^{\circ}$ 时, 点 $C$ 在优弧 $AB$ 上. 当 $\alpha ＞ 90^{\circ}$ 时, 点 $C$ 在劣弧 $AB$ 上.