《2026年金考卷中考试题汇编45套数学山东专版》

22. (本小题满分11分)
已知二次函数$y = ax^{2}-2ax + c$(a,c为常数,$a\neq0$)的最大值为4,且该二次函数图象过点$(2,3)$,与x轴正半轴交于点C,顶点为D,$P(0,t)$是y轴上的动点.
(1) 求该二次函数图象的顶点D的坐标及该二次函数的解析式.
(2) 求当$|PC - PD|$取最大值时,点P的坐标.
(3) $Q(\frac{t}{2},0)$是x轴上的动点,若线段PQ与函数$y = |ax^{2}-2ax + c|$的图象只有一个公共点,请直接写出t的取值范围.

答案：
22
(1)二次函数y = ax² - 2ax + c图象的对称轴为直线x = - $\frac{- 2a}{2a}$ = 1,
∴D(1,4)。(1分)将(1,4),(2,3)分别代入y = ax² - 2ax + c,得$\begin{cases}a - 2a + c = 4\\4a - 4a + c = 3\end{cases}$,解得$\begin{cases}a = - 1\\c = 3\end{cases}$,
∴该二次函数的解析式为y = - x² + 2x + 3。(3分)
(2)令 - x² + 2x + 3 = 0,解得x₁ = - 1,x₂ = 3,
∴C(3,0)。如图
(1),

∵|PC - PD| ≤ CD(提示:三角形两边之差小于第三边),且当P,C,D三点共线时,等号成立,
∴当P,C,D三点共线时,|PC - PD|取得最大值。(5分)设直线CD的解析式为y = kx + b,将C(3,0),D(1,4)分别代入y = kx + b,得$\begin{cases}3k + b = 0\\k + b = 4\end{cases}$,解得$\begin{cases}k = - 2\\b = 6\end{cases}$,
∴直线CD的解析式为y = - 2x + 6,(7分)当x = 0时,y = 6,
∴P(0,6)。(8分)
(3)t ＞ 7,3 ≤ t ＜ 6或t = - 2。(11分)
解法提示:y = |ax² - 2ax + c|可化简为y = $\begin{cases}- x² + 2x + 3(- 1 ≤ x ≤ 3)\\x² - 2x - 3(x ＜ - 1或x ＞ 3)\end{cases}$,其简图如图
(2)所示。

由P(0,t),Q($\frac{t}{2}$,0),易得线段PQ所在直线的解析式为y = - 2x + t。当直线PQ与抛物线y = - x² + 2x + 3只有一个公共点时,令 - 2x + t = - x² + 2x + 3,整理,得x² - 4x + t - 3 = 0,
∴Δ = (- 4)² - 4(t - 3) = 0,解得t = 7。把t = 7代入x² - 4x + t - 3 = 0,得x² - 4x + 4 = 0,解得x₁ = x₂ = 2,- 1 ＜ 2 ＜ 3,符合题意。当线段PQ过点(3,0),即点Q与点(3,0)重合时,t = 6。当线段PQ过点(0,3),即点P与点(0,3)重合时,t = 3。当线段PQ过点(- 1,0),即点Q与点(- 1,0)重合时,t = - 2。结合图象分析可知,当t ＞ 7,3 ≤ t ＜ 6或t = - 2时,线段PQ与函数y = |ax² - 2ax + c|的图象只有一个公共点。

23. (本小题满分11分)
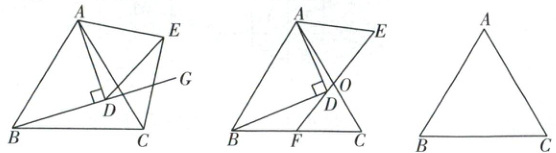
已知$\triangle ABC$是等边三角形,点D在$\triangle ABC$内,且$\angle ADB = 90^{\circ}$,以AD为边在AD右侧作等边三角形ADE.
(1) 如图(1),若点D在射线BG上,连接CE.求$\angle CED$的度数.
(2) 如图(2),延长ED交BC于点F.
① 求证:F是BC的中点.
② 设AC,EF交于点O,若$\cos\angle ABD = \frac{4}{5}$,求$\frac{AO}{OE}$的值.
(3) 连接CE,若$\triangle ABC$的边长是12,点P是CE的中点,请直接写出点B,P之间距离的最大值.

答案：
23
(1)
∵△ABC和△ADE均为等边三角形,
∴∠BAC = ∠DAE = 60°,AB = AC,AD = AE,
∴∠BAD = ∠CAE,
∴△ABD≌△ACE(点拨:“手拉手”模型),
∴∠AEC = ∠ADB = 90°。又
∵∠AED = 60°,
∴∠CED = 90° - 60° = 30°。(3分)
(2)①证明:如图
(1),连接CE,过点C作CQ//BD交EF的延长线于点Q。

同上可知△ABD≌△ACE,∠CED = 30°,
∴BD = CE。
∵∠ADB = 90°,∠ADE = 60°,
∴∠BDF = 180° - 90° - 60° = 30°。又
∵QC//BD,
∴∠Q = ∠BDF = 30°,
∴∠Q = ∠QEC,
∴QC = CE = BD。(4分)又
∵∠QFC = ∠DFB,
∴△CQF≌△BDF,
∴BF = CF,即F为BC的中点。(6分)
②如图
(1),连接AF。
∵△ABC是等边三角形,F是BC的中点,
∴∠CAF = 30° = ∠CEO。又
∵∠AOF = ∠EOC,
∴△AOF∽△EOC,
∴$\frac{AO}{OE}$ = $\frac{AF}{CE}$。(7分)
∵cos∠ABD = $\frac{BD}{AB}$ = $\frac{4}{5}$,
∴设AB = 5a,则CE = BD = 4a,AF = $\frac{\sqrt{3}}{2}$AB = $\frac{5\sqrt{3}}{2}$a,
∴$\frac{AO}{OE}$ = $\frac{AF}{CE}$ = $\frac{\frac{5\sqrt{3}}{2}a}{4a}$ = $\frac{5\sqrt{3}}{8}$。(9分)
(3)3$\sqrt{13}$ + 3。(11分)
解法提示:
方法一:如图
(2),取AC的中点M,连接ME,则ME = $\frac{1}{2}$AC = 6。取MC的中点N,连接NP,则NP = $\frac{1}{2}$ME = 3,
∴点P在以点N为圆心，半径为3的圆上。
又
∵点D在△ABC内部,


∴点P在如图
(3)所示的$\overset{\frown}{TH}$上(提示:找出点D位于临界位置时点P的位置,即可确定点P的运动轨迹)。①当点D在AC上时,点P与点T重合；②当点D在BC上时,点P与点H重合。
连接BN并延长交$\overset{\frown}{TH}$于点P,此时点B,P之间的距离最大。过点N作NS⊥BC于点S。
易知BC = 12,CN = 3,∠ACB = 60°,
∴CS = $\frac{3}{2}$,NS = $\frac{3\sqrt{3}}{2}$,
∴BS = BC - CS = $\frac{21}{2}$,
∴BN = $\sqrt{NS² + BS²}$ = $\sqrt{(\frac{3\sqrt{3}}{2})² + (\frac{21}{2})²}$ = 3$\sqrt{13}$,
∴BP = BN + NP = 3$\sqrt{13}$ + 3,
∴点B,P之间距离的最大值为3$\sqrt{13}$ + 3。
方法二:如图
(4),取AC的中点M,连接MP,则MP//AE,
∴∠MPC = ∠AEC = 90°。取MC的中点N,连接NP,则NP = $\frac{1}{2}$CM = 3。连接BN,同方法一可求得BN = 3$\sqrt{13}$。连接BP,易知BP ≤ BN + NP = 3$\sqrt{13}$ + 3,当点P在BN的延长线上时取等号,
∴点B,P之间距离的最大值为3$\sqrt{13}$ + 3。