《2026年金考卷中考试题汇编45套数学山东专版》

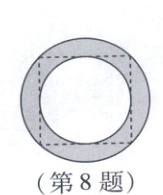
8. 新素材 玉璧 在中国古代文化中,玉璧寓意宇宙的广阔与秩序,也经常被视为君子“修身齐家”的象征.如图是某玉璧的平面示意图,由一个正方形的内切圆和外接圆组成.已知内切圆的半径是2,则图中阴影部分的面积是

A.$\pi$
B.$2\pi$
C.$3\pi$
D.$4\pi$

答案：
8. D
8. D 如图，连接正方形的对角线交于点O，则点O为正方形的内切圆和外接圆的圆心.过O作$OP\perp MN$于点P，则$OP = 2$.易知$\triangle OPN$是等腰直角三角形，$\therefore ON=\sqrt{2}OP=2\sqrt{2}$，$\therefore S_{阴影}=S_{大圆}-S_{小圆}=\pi×(2\sqrt{2})^{2}-\pi×2^{2}=8\pi - 4\pi=4\pi$。

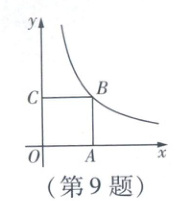
9. 如图,在平面直角坐标系中,A,C两点在坐标轴上,四边形OABC是面积为4的正方形.若函数$y=\frac{k}{x}(x＞0)$的图象经过点B,则满足$y\ge2$的x的取值范围为

A.$0 ＜ x\le2$
B.$x\ge2$
C.$0 ＜ x\le4$
D.$x\ge4$

答案： 9. A
9. A $\because$正方形OABC的面积为4，$\therefore AB = BC = 2$，$AB\perp x$轴，$BC\perp y$轴，$\therefore B(2,2)$.观察题中函数图象可知，满足$y\geq2$的x的取值范围为$0＜x\leq2$.故选A.

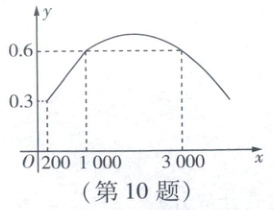
10. 新课标 跨学科试题 在水分、养料等条件一定的情况下,某植物的生长速度y(厘米/天)和光照强度x(勒克斯)之间存在一定关系.在低光照强度范围$(200\le x ＜ 1000)$内,y与x近似成一次函数关系;在中高光照强度范围$(x\ge1000)$内,y与x近似成二次函数关系.其部分图象如图所示.根据图象,下列结论正确的是

A.当$x\ge1000$时,y随x的增大而减小
B.当$x = 2000$时,y有最大值
C.当$y\ge0.6$时,$x\ge1000$
D.当$y = 0.4$时,$x = 600$

答案：
10. B
10. B
名师教解题
此段为二次函数图象，当$x\geq1000$时，y随x的增大先增大再减小，故A项错误
对于D项，画出直线$y = 0.4$，发现其与函数图象有2个交点，故x的值有2个，故D项错误
直线$x=\frac{1000 + 3000}{2}=2000$为抛物线的对称轴，
$\therefore$当$x = 2000$时，y有最大值，故B项正确
$y\geq0.6$，即直线$y = 0.6$上方（含直线）的抛物线，其对应的x的取值范围是$1000\leq x\leq3000$，故C项错误

11. 新课标 开放性试题 写出使分式$\frac{1}{2x - 3}$有意义的x的一个值:0（答案不唯一，满足$x\neq\frac{3}{2}$即可）.

答案： 11. 0（答案不唯一，满足$x\neq\frac{3}{2}$即可）

12. 在平面直角坐标系中,将点$P(3,4)$向下平移2个单位长度,得到的对应点$P'$的坐标是(3,2).

答案： 12. $(3,2)$

13. 若关于x的一元二次方程$x^{2} + 4x - m = 0$有两个不相等的实数根,则实数m的取值范围是$m＞-4$.

答案： 13. $m＞-4$
【解析】$\because$方程$x^{2}+4x - m = 0$有两个不相等的实数根，
$\therefore\Delta=4^{2}-4×1×(-m)＞0$，$\therefore m＞-4$.

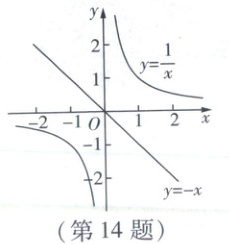
14. 如图,取直线$y = -x$上一点$A_{1}(x_{1},y_{1})$,①过点$A_{1}$作x轴的垂线,交$y=\frac{1}{x}$的图象于点$A_{2}(x_{2},y_{2})$;②过点$A_{2}$作y轴的垂线,交直线$y = -x$于点$A_{3}(x_{3},y_{3})$……如此循环进行下去.按照上面的操作,若点$A_{1}$的坐标为$(1,-1)$,则点$A_{2025}$的坐标是$(1,-1)$.

答案：
14. $(1,-1)$
【解析】根据题意画出图形，如图所示，由$A_{1}(1,-1)$，得$A_{2}(1,1)$，$A_{3}(-1,1)$，$A_{4}(-1,-1)$，$A_{5}(1,-1)$，$·s$，$\therefore$四个点为一个循环.$\because2025÷4 = 506·s·s1$，$\therefore$点$A_{2025}$的坐标与点$A_{1}$的坐标相同，$\therefore A_{2025}(1,-1)$.

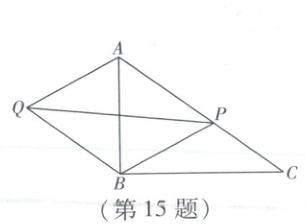
15. 如图,在$Rt\triangle ABC$中,$\angle ABC = 90^{\circ},AB = 6,BC = 8$,点P为边AC上异于点A的一点,以PA,PB为邻边作$□ PAQB$,则线段PQ的最小值是$\frac{24}{5}$.

答案：
15.
名师教审题
几何综合题系列
如图，在$Rt\triangle ABC$中，$\angle ABC = 90^{\circ}$，$AB = 6$，$BC = 8$，点P为边AC上异于点A的一点，以PA，PB为邻边作$□ PAQB$，则线段PQ的最小值是多少。
【解析】在$Rt\triangle ABC$中，由勾股定理得$AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{6^{2}+8^{2}} = 10$.设PQ与AB交于点O.$\because$四边形PAQB是平行四边形，$\therefore AO = BO=\frac{1}{2}AB = 3$，$PQ = 2OP$，$\therefore$当OP的值最小时，PQ的值最小.易知当$OP\perp AC$时，OP的值最小（点拨：垂线段最短），此时PQ的值最小，如图所示.
$\because\sin\angle BAC=\frac{OP}{AO}=\frac{BC}{AC}$，$\therefore \frac{OP}{3}=\frac{8}{10}$，$\therefore OP=\frac{12}{5}$，$\therefore$线段PQ的最小值为$2OP=\frac{24}{5}$.