《2026年金考卷中考试题汇编45套数学山东专版》

1. $-\frac{1}{2025}$的相反数是 (C)

A.2025
B.-2025
C.$\frac{1}{2025}$
D.$-\frac{1}{2025}$

答案： 1 C

2. 新素材 世界第一“大碗” 如图是世界第一“大碗”——景德镇昌南里文化艺术中心主体建筑,其造型灵感来自宋代湖田窑影青斗笠碗,寓意“万瓷之母”.关于它的三视图,下列说法正确的是 (A)

A.主视图和左视图相同
B.主视图和俯视图相同
C.俯视图和左视图相同
D.三种视图均相同

答案： 2 A

3. 2024年山东集中支持汽车、家电等8个领域消费品以旧换新工作,合计带动销售1270亿元左右,汽车报废更新49.2万辆,居全国首位.将数据“49.2万”用科学记数法表示为 (B)

A.$49.2×10^{4}$
B.$4.92×10^{5}$
C.$492×10^{4}$
D.$4.92×10^{4}$

答案： 3 B

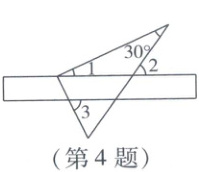
4. 将一把直尺与一块含有$30^{\circ}$角的直角三角板按如图方式放置,若$∠3 = 65^{\circ}$,则$∠2$的度数为 (B)

A.$50^{\circ}$
B.$55^{\circ}$
C.$60^{\circ}$
D.$65^{\circ}$

答案：
4 B 如图,$\because AB // CD$,$\therefore \angle 4=\angle 3=65^{\circ}$(依据：两直线平行，同位角相等），$\therefore \angle 1=90^{\circ}-65^{\circ}=25^{\circ}$,$\therefore \angle 2=\angle 1+30^{\circ}=25^{\circ}+30^{\circ}=55^{\circ}$（依据：三角形的外角等于与它不相邻的两个内角的和）。

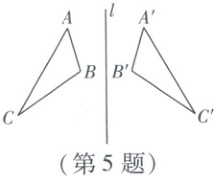
5. 如图,$△ABC$与$△A'B'C'$关于直线$l$对称,$∠A = 45^{\circ}$,$∠B' = 110^{\circ}$,则$∠C$的度数为 (C)

A.$15^{\circ}$
B.$20^{\circ}$
C.$25^{\circ}$
D.$35^{\circ}$

答案： 5 C $\because \triangle ABC$与$\triangle A'B'C'$关于直线$l$对称，$\angle B' = 110^{\circ}$,$\therefore \angle B = \angle B' = 110^{\circ}$.又$\because \angle A = 45^{\circ}$,$\therefore \angle C = 180^{\circ} - \angle A - \angle B = 180^{\circ} - 45^{\circ} - 110^{\circ} = 25^{\circ}$.

6. 下列各式计算正确的是 (D)

A.$a^{3} + a^{4} = 2a^{7}$
B.$(a - b)^{2} = a^{2} - b^{2}$
C.$(-ab^{3})^{3} = a^{3}b^{9}$
D.$3a(1 - a) = 3a - 3a^{2}$

答案： 6 D 逐项分析如下,故选D.
选项 分析 正误
A $a^{3}$与$a^{4}$不是同类项,不能合并. $×$
B $(a - b)^{2} = a^{2} - 2ab + b^{2}$ $×$
C $(-ab^{3})^{3} = -a^{3}b^{9}$ $×$
D $3a(1 - a) = 3a - 3a^{2}$ $\surd$

7. 已知关于$x$的一元二次方程$x^{2} + 5x - m = 0$的一个根是-6,则另一个根是 (D)

A.-2
B.2
C.-1
D.1

答案： 7 D 方法一:设该方程的另一个为$t$,则$-6 + t = -5$（点拨:根与系数的关系）,解得$t = 1$,即该方程的另一个根为1.方法二:$\because$关于$x$的一元二次方程$x^{2} + 5x - m = 0$的一个根是$-6$,$\therefore 36 - 30 - m = 0$,$\therefore m = 6$,$\therefore$原方程为$x^{2} + 5x - 6 = 0$,解得$x_{1} = -6,x_{2} = 1$,即该方程的另一个根为1.

8. 学校招募运动会服务志愿者,从报名的甲、乙、丙、丁四位同学中随机选取两人,则选取的两人中有乙同学的概率为 (C)

A.$\frac{3}{4}$
B.$\frac{2}{3}$
C.$\frac{1}{2}$
D.$\frac{1}{3}$

答案： 8 C 列表如下:
甲 乙 丙 丁
甲 (乙,甲) (丙,甲) (丁,甲)
乙 (甲,乙) (丙,乙) (丁,乙)
丙 (甲,丙) (乙,丙) (丁,丙)
丁 (甲,丁) (乙,丁) (丙,丁)
由表格可知,共有12种等可能的结果,其中选取的两人中有乙同学的结果有6种,故所求概率为$\frac{6}{12} = \frac{1}{2}$.