《2026年金考卷中考试题汇编45套数学山东专版》

23. (本小题满分11分)
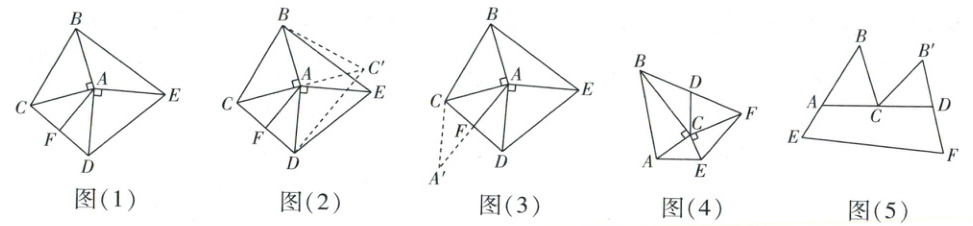
(1)如图(1),已知$△ABC$,$△ADE$,$∠BAC = ∠DAE = 90^{\circ}$,$AB = AC$,$AD = AE$,连接$CD$,$BE$,$F$为$CD$的中点,连接$AF$,求证:$2AF = BE$.
小明、小亮两位同学针对题目中的中点条件给出了两种处理策略.
小明的思路如下:如图(2),延长$CA$至点$C'$,使得$AC' = AC$,连接$BC'$,$DC'$,可证$△ABE≌△$AC'D.
$\because A$为$CC'$的中点,$\therefore AF$为$△CC'D$的中位线,$\therefore 2AF =$C'D$ = BE$.
小亮的思路如下:如图(3),延长$AF$至点$A'$,使得$A'F = AF$,可证$△AFD≌△A'FC$,$A'C// AD$,
$\therefore ∠A'CA + ∠CAD = 180^{\circ}$,$\therefore ∠A'CA = ∠$EAB,可证$△ABE≌△$CAA',$\therefore 2AF = AA' = BE$.
(2)如图(4),在$Rt△ABC$中,$∠ACB = 90^{\circ}$,$2AC = BC$,在$Rt△ECF$中,$∠ECF = 90^{\circ}$,$2EC = FC$,连接$BF$,$AE$,$D$为$BF$的中点,连接$CD$,请求出线段$CD$与线段$AE$的数量关系.
(3)如图(5),$△ABC$中,$∠BAC = 60^{\circ}$,$AC = 2$,点$E$在射线$BA$上,$BE = 4$,延长$AC$至点$D$,使得$AD = 4$,将边$BC$绕点$C$顺时针旋转$60^{\circ}$至$B'C$,连接$B'D$并延长至点$F$,使得$D$为$B'F$的中点,连接$EF$,求线段$EF$的最小值.

答案：
23
(1)$AC'D C'D EAB CAA'$ (4分)
(2)方法一:如图
(1),延长$BC$至点$B'$,使得$B'C = BC$,连接$AB'$,$B'F$.
$\because D$为$BF$的中点,
$\therefore 2CD = B'F$(依据:中位线定理).(5分)
在$\triangle ACE$和$\triangle B'CF$中,
$\angle ACE = \angle B'CF = 90^{\circ} - \angle ECB'$,
$\frac{AC}{CB'} = \frac{CE}{CF} = \frac{1}{2}$,
$\therefore \triangle ACE \sim \triangle B'CF$(点拨:手拉手相似模型),
$\therefore \frac{AE}{B'F} = \frac{CE}{CF} = \frac{1}{2}$,$\therefore 2AE = B'F$,(7分)
$\therefore AE = CD$.

方法二:如图
(2),延长$CD$至点$C'$,使得$C'D = CD$,连接$C'F$.
$\because D$为$BF$的中点,$\therefore BD = FD$.
又$\because \angle BDC = \angle FDC'$,
$\therefore \triangle BCD \cong \triangle FC'D(SAS)$,
$\therefore BC = FC'$,$\angle C = \angle DC'F$,$\therefore BC // FC'$,
$\therefore \angle BCF + \angle ACE = 180^{\circ}$,$\therefore \angle C'FC + \angle BCF = 180^{\circ}$.
$\because \angle BCF + \angle ACE = 180^{\circ}$,$\therefore \angle C'FC = \angle ACE$.
在$\triangle FCC'$和$\triangle CEA$中,
$\angle C'FC = \angle ACE$,$2EC = FC$,$FC' = BC = 2AC$,
即$\frac{FC'}{AC} = \frac{FC}{CE} = 2$,
$\therefore \triangle FCC' \sim \triangle CEA$,
$\therefore \frac{FC'}{AE} = \frac{FC}{CE} = 2$,$\therefore C'C = 2AE = 2CD$,$\therefore AE = CD$.(8分)
(3)如图
(3),连接$CE$,$CF$,延长$B'C$至点$G$,使得$CG = B'C$,连接$GF$,

则$GF = 2CD = EB$,$GF // CD$,
$\therefore \angle CGF = \angle B'CD$.
由旋转的性质,得$CB = CB' = CG$,$\angle BCB' = 60^{\circ} = \angle BAC$,
$\therefore \angle BCD = \angle B'CD + 60^{\circ} = \angle ABC + 60^{\circ}$,
$\therefore \angle B'CD = \angle ABC$,$\therefore \angle CGF = \angle ABC$,
$\therefore \triangle CGF \cong \triangle CBE(SAS)$,$\therefore CE = CF$,$\angle GCF = \angle BCE$,
$\therefore \angle ECF = \angle BCG = 120^{\circ}$.
过点$C$作$CH \perp EF$于点$H$,则$\angle ECH = 60^{\circ}$,
$\therefore EF = 2EH = \sqrt{3}CE$,
$\therefore$当$CE$最小时,线段$EF$取得最小值(关键点:将求线段$EF$的最小值转化为求线段$CE$的最小值).
过点$C$作$CE' \perp AB$于点$E'$,则$CE' = \frac{\sqrt{3}}{2}AC = \sqrt{3}$.
$\because$点$E$在射线$BA$上,
$\therefore$当$CE \perp AB$,即点$E$与点$E'$重合时,$CE$取得最小值,最小值为$\sqrt{3}$(点拨:垂线段最短),
$\therefore$线段$EF$的最小值为$\sqrt{3}CE = 3$.(11分)
更多讲解详见《解题有招》折页“快招4”
名师辨模型
常见的中点模型
作法说明 图示
见中线,可倍长
倍长中线或类中线(与中点有关的线段)构造全等三角形或平行四边形。

见等腰三角形,想“三线合一”
已知等腰三角形底边的中点,可以考虑与顶点相连,用“三线合一”解题。

见斜边,想中线
已知直角三角形斜边的中点,可以考虑构造斜边上的中线,目的是得到三条相等的线段和两对等角。

续表
作法说明 图示
见一个或多个中点,想中位线
已知三角形两边的中点,可以连接这两个中点,构造中位线。

已知一边中点,可以在其他边上取中点,连接两个中点构造中位线。

已知三角形的一条中线,通过倍长三角形的一边,构造一个大三角形,使原三角形的中线变为大三角形的中位线。