《2026年金考卷中考试题汇编45套数学山东专版》

1. $\sqrt{4}$的相反数是 (A)

A.$-2$
B.$\pm 2$
C.$4$
D.$\pm 4$

答案： 1 A

2. 下列图形中既是轴对称图形又是中心对称图形的是 (D)

答案： 2 D 逐项分析如下,故选 D. 选项 分析 是否符合题意 A 不是轴对称图形,是中心对称图形. 否 B 既不是轴对称图形,也不是中心对称图形. 否 C 不是轴对称图形,是中心对称图形. 否 D 既是轴对称图形,又是中心对称图形. 是

3. 科学家通过观测宇宙背景辐射的温度变化来推测光的传播方式以及宇宙的形状.在宇宙中,宇宙背景辐射分布得非常均匀,但不同区域的宇宙背景辐射仍存在微小的温度差异,热点和冷点之间的温差约为$0.0002^{\circ}C$.$0.0002$用科学记数法记为 (C)

A.$0.2× 10^{-4}$
B.$2× 10^{-3}$
C.$2× 10^{-4}$
D.$2× 10^{-5}$

答案： 3 C

4. 下列几何体均是由若干个大小相同的小正方体搭建而成的,其主视图是如图所示图形的是 (C)

答案：
4 C 逐项分析如下,故选 C.

5. 下列运算中不正确的是 (D)

A.$2a^{2}· 3a^{3}=6a^{5}$
B.$(-4a^{2}b)^{2}=16a^{4}b^{2}$
C.$3a - a = 2a$
D.$(-2a)^{3}÷ a = 8a^{2}$

答案： 5 D 逐项分析如下,故选 D. 选项 分析 正误 A $2a^{2} · 3a^{3}=(2 × 3) · a^{2+3}=6a^{5}$ √ B $(-4a^{2}b)^{2}=(-4)^{2} · a^{2 × 2} · b^{2}=16a^{4}b^{2}$ √ C $3a - a = 2a$ √ D $(-2a)^{3} ÷ a=-8a^{3} ÷ a=-8a^{2}$ ×

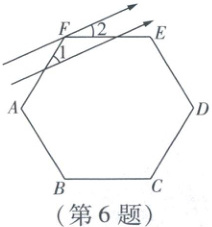
6. 如图,一束平行光线照射到正六边形$ABCDEF$上,若$\angle 1 = 35^{\circ}$,则$\angle 2 = $ (B)

A.$15^{\circ}$
B.$25^{\circ}$
C.$35^{\circ}$
D.$37^{\circ}$

答案：
6 B 如图,
∵ 六边形 ABCDEF 是正六边形,
∴ ∠AFE = $\frac{(6 - 2) × 180^{\circ}}{6}=120^{\circ}$,
∴ ∠3 = $180^{\circ}- ∠1 - ∠AFE = 25^{\circ}$.
∵ 光线互相平行,
∴ ∠2 = ∠3 = $25^{\circ}$,故选 B.

7. 有4张看上去无差别的卡片,上面分别写着$1,3,5,7$.随机抽取1张后,放回并混在一起,再随机抽取1张,那么两次抽取的卡片上数字之和能被3整除的概率是 (D)

A.$\frac{1}{3}$
B.$\frac{5}{6}$
C.$\frac{5}{8}$
D.$\frac{5}{16}$

答案： 7 D 列表如下： 1 3 5 7 1 (1,1) (3,1) (5,1) (7,1) 3 (1,3) (3,3) (5,3) (7,3) 5 (1,5) (3,5) (5,5) (7,5) 7 (1,7) (3,7) (5,7) (7,7) 由表格可知共有 16 种等可能的结果,其中两次抽取的卡片上数字之和能被 3 整除的结果有 5 种,故所求概率是$\frac{5}{16}$.故选 D.

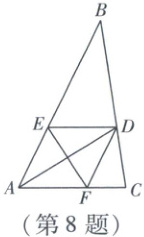
8. 在$\triangle ABC$中,作$\angle BAC$的平分线交$BC$于点$D$,作$AD$的垂直平分线分别交$AB$于点$E$,交$AC$于点$F$,连接$DE,DF$,得到四边形$AEDF$.若$AE = 4$,则四边形$AEDF$的周长为 (A)

A.$16$
B.$8\sqrt{3}$
C.$8 + 4\sqrt{3}$
D.$8 + 8\sqrt{3}$

答案：
8 A 如图,设 AD 与 EF 交于点 O.
∵ AD 平分 ∠BAC,
∴ ∠EAD = ∠FAD.
∵ EF 是 AD 的垂直平分线,
∴ AE = DE, AF = DF(依据：线段垂直平分线上的点到线段两端的距离 相等 ),∠AOE = ∠AOF = $90^{\circ}$.在 △AOE 和 △AOF 中, $\begin{cases} ∠EAO = ∠FAO, \\ AO = AO, \\ ∠AOE = ∠AOF, \end{cases}$
∴ △AOE≌△AOF,
∴ AE = AF,
∴ DF = AF = AE = DE = 4,
∴ 四边形 AEDF 是菱形 (依据：四条边相等的 四边形是菱形 ),
∴ 菱形 AEDF 的周长为 4 × 4 = 16.故选 A.