《2026年金考卷中考试题汇编45套数学山东专版》

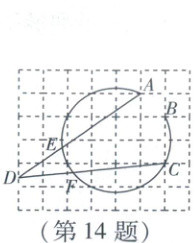
14. 如图是由边长为1的小正方形组成的网格,$\overset{\LARGE{\frown}}{ACB}$上的点A,B,C均为格点(网格线的交点),点D网格线上一点,连接AD,CD,分别交$\overset{\LARGE{\frown}}{ACB}$于点E,F.若$\angle ADC = 30^{\circ}$,则$\overset{\LARGE{\frown}}{EF}$的长为$\frac{\sqrt{5}π}{6}$(结果保留$\pi$).

答案：
14 $\frac{\sqrt{5}π}{6}$
[解析]如图，易知点O为ACB所在圆的圆心,连接OA,OC,则∠AOC=90°,OA=√5.连接EC,则∠AEC=
$\frac{1}{2}$∠AOC=45°,
∴∠ECD=∠AEC−∠ADC=45°−30°=
15°,
∴EF所对的圆心角为2×15°=30°,
∴EF的长为$\frac{30π×\sqrt{5}}{180}$=$\frac{\sqrt{5}π}{6}$.

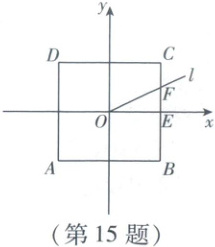
15. 如图,在平面直角坐标系中,正方形ABCD的中心位于原点O,$AB = 4$,$BC\perp x$轴于点E,F为CE的点.射线l的端点为O,将射线l从与OF重合的位置开始绕点O逆时针旋转,每次旋转$45^{\circ}$,则2 026次旋转结束时,射线l与正方形ABCD的边的交点坐标为(-1,2).

答案：
15 (−1,2)
[解析]
∵正方形ABCD的中心位于原点O,BC⊥x轴，
AB=4,
∴C(2,2),CE=2,
∴CF=EF=1.
∵射线l从与OF 重合的位置开始绕点O逆时针旋转，每次旋转45°,360°÷45°=8,
∴射线l每旋转8次为一个循环.又2026÷8=
253……2,
∴射线l第2026次旋转结束时的位置与第2次旋转结束时的位置相同，如图所示，设射线l与CD边交于点H,CD与y轴交于点M,易证△OMH≌△OEF,
∴HM=
EF=1,
∴H(−1,2).

16. (本题每小题4分,共8分)
(1) 计算: $3×\sqrt[3]{27}+(1+\pi)^{0}-(\cos60^{\circ})^{-1}$.
(2) 解分式方程: $\frac{1 - x}{x - 3}=\frac{x}{2x - 6}-1$.

答案： 16
(1)原式=3×3+1−2
=8.
(2)去分母,得2(1−x)=x−(2x−6),
去括号,得2−2x=x−2x+6,
移项、合并同类项,得−x=4,
系数化为1,得x=−4.
检验,当x=−4时,2x−6≠0.
∴x=−4是原分式方程的解.

17. (本小题满分8分)
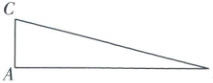
如图,在$Rt\triangle ABC$中,$\angle A = 90^{\circ}$,$\angle B = 15^{\circ}$.
(1) 请用无刻度的直尺和圆规作BC的垂直平分线,交BC于点E,交AB于点D(不要求写作法,保作图痕迹).
(2) 求$\tan\angle ACB$的值.

答案：
17
(1)如图
(1),直线MN即为所求作的垂直平分线.

(2)如图
(2),连接CD.
∵MN垂直平分线段BC，
∴DC=DB,
∴∠1=∠B=15°,
∴∠2=∠1+∠B=30°,
∴BD=CD=2AC,AD=√3AC,
∴AB=(√3+2)AC,
∴tan∠ACB=$\frac{AB}{AC}$=√3+2.

18. (本小题满分8分)
某影院正在热映一部爱国题材的影片.已知小明(儿童)一家三口(爸爸、妈妈和小明)去观看该影片,共花费160元;小英(儿童)和她妈妈一起去观看该影片,共花费100元.该影片的票价分成人票价和儿童票价,上述两次消费均不含其他费用.
(1) 求该影院该影片的成人票和儿童票的单价.
(2) 某校为通过该片传递的正能量,激励师生传承和弘扬中华优秀传统文化,特组织全校1 800名师生(学生均为儿童)集体到该影院观看该影片.影院特推出两种优惠活动(只能选其中一种):
活动一:成人票的单价打八折,儿童票的单价打六折;
活动二:成人票按原价,儿童团体票每购买满300张赠200张(赠票不得有余票).
①设教师人数为x(人),总费用为y(元).若按活动一购买,求y与x之间的函数关系式;
②若该校由200名教师带领学生观影,请判断采用哪种活动购票能使花费最少,并说明理由.

答案： 18
(1)设该影院该影片成人票的单价为a元，儿童票的单价为b元.
根据题意，得{2a+b=160, a+b=100,
解得{a=60, b=40.
答:该影院该影片成人票的单价为60元，儿童票的单价为40元.
(2)①由题意可知,y=60x×0.8+(1800−x)×40×0.6=
24x+43200.
②按活动一购票能使花费最少.
理由:由题意可知,若采用活动一购票，则y=200×24+43200=48000(元).
若采用活动二购票，则购买成人票共花费60×200=12000(元)，
购买儿童票共花费(3×300+100)×40=40000(元)(点拨:要购买1600张儿童票，可买3个300人的团体票，得1500张票，再购买100张儿童票即可)，
∴总费用为12000+40000=52000(元).
∵48000＜52000,
∴活动一购票能使花费最少.