《2026年金考卷中考试题汇编45套数学山东专版》

9. 如图，在$\triangle ABC$中，按如下步骤作图：
①在$CA$和$CB$上分别截取$CM$，$CN$，使$CM = CN$，分别以点$M$和$N$为圆心，以大于$\frac{1}{2}MN$的长为半径作弧，两弧在$\angle ACB$内交于点$O$，作射线$CO$交$AB$于点$D$；
②分别以点$C$和$D$为圆心，大于$\frac{1}{2}CD$的长为半径作弧，两弧相交于点$P$和$Q$，作直线$PQ$交$AC$于点$E$，交$BC$于点$F$。
根据以上作图，若$AD = 4$，$DB = 2$，$BC = 3\sqrt{2}$，则线段$AE$的长为(D)


A.$\frac{11\sqrt{2}}{3}$
B.$\frac{11}{2}$
C.5
D.$4\sqrt{2}$

答案：
9 D
快招解题法 试题秒解 考场速用
如图,连接 DE(或 DF,关键辅助线),由题意可知 CD 平分$\angle ACB$,$EF$垂直平分线段 CD(依据:线段垂直平分线上的点到线段两端的距离相等),
$\therefore\angle ECD=\angle EDC,\therefore\angle FCD=\angle EDC,\therefore DE// BC,\therefore\triangle ADE\backsim\triangle ABC$(点拨:“A”字型相似模型).
$\therefore\frac{AD}{AB}=\frac{DE}{BC}=\frac{AE}{AC}$.
$\because AD = 4,DB = 2,BC = 3\sqrt{2},\therefore\frac{4}{4 + 2}=\frac{DE}{3\sqrt{2}}$,
$\therefore DE = 2\sqrt{2},\therefore CE = DE = 2\sqrt{2}$.
$\therefore\frac{AE}{AE + 2\sqrt{2}}=\frac{4}{6},\therefore AE = 4\sqrt{2}$.故选 D.

更多讲解详见《解题有招》折页“快招 2”

10. 已知二次函数$y = ax^{2} + bx + c$($a$，$b$，$c$为常数，$a \neq 0$)图象的顶点坐标是$(-1,n)$，且经过$(1,0)$，$(0,m)$两点，$3 ＜ m ＜ 4$。有下列结论：
①关于$x$的一元二次方程$ax^{2} + bx + c - n + 1 = 0$($a \neq 0$)有两个不相等的实数根；②当$x ＞ -1$时，$y$的值随$x$值的增大而减小；③$-\frac{4}{3} ＜ a ＜ -1$；④$4a - 2b + c ＞ 0$；⑤对于任意实数$t$，总有$(t + 1)(at - a + b) \leq 0$。
以上结论正确的有(A)

A.5个
B.4个
C.3个
D.2个

答案：
10 A 由二次函数$y = ax^{2} + bx + c$图象的顶点坐标是$(-1,n)$,且经过点$(1,0),(0,m)$可知,抛物线的对称轴为直线$x = - 1$,且开口向下,$\therefore a ＜ 0$,抛物线与$x$轴的另一交点坐标为$(-3,0)$,画出大致图象如图所示.逐个分析如下:

序号 分析 正误
① 由函数图象可知,抛物线$y = ax^{2} + bx + c$与直线$y = n - 1$有两个交点,$\therefore$方程$ax^{2} + bx + c = n - 1(a\neq0)$有两个不相等的实数根. √
② $\because$抛物线开口向下,对称轴为直线$x = - 1$,$\therefore$当$x ＞ - 1$时,$y$的值随$x$值的增大而减小. √
③ $\because$抛物线与$x$轴的交点坐标为$(1,0),(-3,0)$,$\therefore y = a(x - 1)(x + 3)=ax^{2}+2ax - 3a,\therefore m = - 3a.\because3 ＜ m ＜ 4,\therefore3 ＜ - 3a ＜ 4,\therefore - \frac{4}{3} ＜ a ＜ - 1$. √
④ 结合函数图象可知,当$x = - 2$时,$y = 4a - 2b + c ＞ 0$. √
⑤ $\because - \frac{b}{2a} = - 1,\therefore b = 2a,\therefore(t + 1)(at - a + b)=(t + 1)(at - a + 2a)=(t + 1)(at + a)=a(t + 1)(t + 1)=a(t + 1)^{2},\because a ＜ 0,(t + 1)^{2}\geq0,\therefore a(t + 1)^{2}\leq0$,即对于任意实数$t,(t + 1)(at - a + b)\leq0$. √
综上,结论①②③④⑤正确,故选 A.

11. 已知一个正方形的面积为2，则其边长为$\sqrt{2}$。

答案： 11$\sqrt{2}$

12. 在一个不透明的袋中有2个红球、3个黄球和4个白球，这些球除颜色外都相同。从中随机摸出一个球，这个球是红球的概率为$\frac{2}{9}$。

答案： 12$\frac{2}{9}$

13. 如图，两条直线$l_{1}$，$l_{2}$分别经过正六边形$ABCDEF$的顶点$B$，$C$，且$l_{1} // l_{2}$。当$\angle 1 = 37^{\circ}$时，$\angle 2 =$97$^{\circ}$。

答案：
13 97
[解析]如图,$\because\angle ABC=\frac{(6 - 2)×180^{\circ}}{6}=120^{\circ},\angle1 = 37^{\circ}$,
$\therefore\angle3=\angle ABC - \angle1 = 120^{\circ}-37^{\circ}=83^{\circ}.\because l_{1}// l_{2}$,
$\therefore\angle3+\angle2 = 180^{\circ},\therefore\angle2 = 180^{\circ}-\angle3 = 97^{\circ}$.

14. $A$，$B$两地相距100 km，甲、乙两人骑车同时分别从$A$，$B$两地相向而行。假设他们都保持匀速行驶，甲、乙两人各自到$A$地的距离$s$(km)与骑车时间$t$(h)的关系如图所示，则他们相遇时距离$A$地$\frac{300}{7}$km。

答案： 14$\frac{300}{7}$
[解析]结合题图可设$s_{甲}=k_{1}t,s_{乙}=k_{2}t + 100$,将$(2,30)$,$(1,80)$分别代入$s_{甲}=k_{1}t,s_{乙}=k_{2}t + 100$,得$k_{1}=15,k_{2}=-20$,
$\therefore s_{甲}=15t,s_{乙}=-20t + 100$.令$15t=-20t + 100$,解得$t=\frac{20}{7}$,
$\therefore s=\frac{300}{7}$,即他们相遇时距离 A 地$\frac{300}{7}km$.

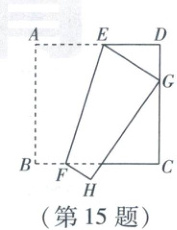
15. 如图，正方形纸片$ABCD$中，$E$是$AD$上一点，将纸片沿过点$E$的直线折叠，使点$A$落在$CD$上的点$G$处，点$B$落在点$H$处，折痕$EF$交$BC$于点$F$。若$CG = 4$，$EF = 4\sqrt{3}$，则$AB =$$2 + 2\sqrt{5}$。

答案：
15$2 + 2\sqrt{5}$
[解析]如图,连接 AG 交 EF 于点 M,过点 F 作$FN\perp AD$,垂足为 N.
$\because\angle FNA=\angle FNE = 90^{\circ}$.
$\because$四边形 ABCD 是正方形,
$\therefore AB = AD = CD,\angle BAD=\angle ABC=\angle D = 90^{\circ}$.
$\therefore$四边形 ABFN 是矩形(依据:有三个角是直角的四边形是矩形),
$\therefore NF = AB = AD$.
由折叠可知$AG\perp EF,\therefore\angle GAE=\angle NFE$.
又$\because\angle FNE=\angle D = 90^{\circ},\therefore\triangle ADG\cong\triangle FNE$(ASA)(点拨:“十”字全等模型),
$\therefore AG = EF = 4\sqrt{3}$.
设$AB = AD = CD = x$,则$DG = CD - CG = x - 4$.
在$Rt\triangle ADG$中,$DG^{2}+AD^{2}=AG^{2}$,即$(x - 4)^{2}+x^{2}=(4\sqrt{3})^{2}$,
解得$x_{1}=2 + 2\sqrt{5},x_{2}=2 - 2\sqrt{5}$(舍去),
$\therefore AB = 2 + 2\sqrt{5}$.
巧作辅助线:作 2 条辅助线,构造“十”字全等模型.

名师讲方法
解题突破本题的关键在于结合题目条件,通过作辅助线,构造全等三角形,再利用勾股定理,求 AB 的长.

16. （本小题满分7分）
计算：$(\pi - 3)^{0} + (\frac{1}{2})^{-1} + | - 5 | + 2\sin 45^{\circ} - \sqrt{8}$。

答案： 16 原式$=1 + 2 + 5 + 2×\frac{\sqrt{2}}{2}-2\sqrt{2}$
$=8+\sqrt{2}-2\sqrt{2}$
$=8-\sqrt{2}$.