《2026年金考卷中考试题汇编45套数学山东专版》

22. （本小题满分10分）
随着“体重管理年”三年行动的实施，全民体重管理意识和技能逐步提升。某健身中心要采购甲、乙两种型号的健身器材以满足群众的健身需求。据了解，甲型健身器材的单价比乙型健身器材的单价低300元，用50 000元购买甲型健身器材的数量和用56 000元购买乙型健身器材的数量相同。
(1)求甲、乙两种型号健身器材的单价分别是多少元。
(2)该健身中心计划购买甲、乙两种型号的健身器材共20台，且甲型健身器材的购买数量不超过乙型健身器材购买数量的3倍，购买甲型健身器材多少台时采购费用最少？最少采购费用是多少元？

答案：
(1)设甲种型号的健身器材的单价为$x$元/台,则乙种型号的健身器材的单价为$(x + 300)$元/台,
根据题意,得$\frac{50000}{x}=\frac{56000}{x + 300}$,
解得$x = 2500$,
检验,当$x = 2500$时,$x(x + 300)\neq0$,且符合题意(点拨:易失分点,解分式方程时一定要验根),
此时$x + 300 = 2800$.
答:甲种型号的健身器材的单价为 2500 元/台,乙种型号的健身器材的单价为 2800 元/台.
(2)设购买甲种型号的健身器材$a$台,则购买乙种型号的健身器材$(20 - a)$台,
根据题意,得$a\leq3(20 - a)$,解得$a\leq15$.
设采购费用为$w$元,
根据题意,得$w = 2800(20 - a)+2500a=-300a + 56000$,
$\because k=-300＜0,\therefore w$随$a$的增大而减小,
$\therefore$当$a = 15$时,$w$取最小值,最小值为$-300×15 + 56000 = 51500$.
答:购买甲种型号的健身器材 15 台,采购费用最少,最少费用为 51500 元.

23. （本小题满分10分）
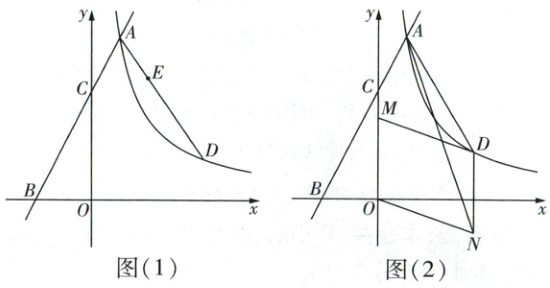
一次函数$y = 2x + 4$的图象与反比例函数$y = \frac{k}{x}$（$x ＞ 0$）的图象交于点$A(m,6)$，与$x$轴交于点$B$，与$y$轴交于点$C$。
(1)求$m$，$k$的值。
(2)$D$为反比例函数图象上的一点且横坐标大于$m$。
①如图(1)，若点$D$的横坐标为4，连接$AD$，$E$为线段$AD$上一点，且$\frac{AE}{ED} = \frac{1}{2}$，求点$E$的坐标；
②如图(2)，$M$为线段$OC$上一点，且$CM = 1$，四边形$OMDN$是平行四边形，连接$AN$，若$\angle BAN = 45^{\circ}$，求点$D$的坐标。

答案：
23
(1)$\because$点$A(m,6)$在一次函数$y = 2x + 4$的图象上,
$\therefore6 = 2m + 4$,解得$m = 1$.
$\because$点$A(1,6)$在反比例函数$y=\frac{k}{x}$的图象上,
$\therefore6=\frac{k}{1}$,解得$k = 6$.
(2)①如图
(1),过点 A 作$AF\perp x$轴于点 F,分别过点 E,D 作$EG\perp AF$于点 G,$DH\perp AF$于点 H,则$EG// DH$,

$\therefore\triangle GAE\backsim\triangle HAD$(点拨:“A”字型相似模型),
$\therefore\frac{AG}{AH}=\frac{GE}{HD}=\frac{AE}{AD}=\frac{1}{3}$.
由
(1)知$y=\frac{6}{x}$,将$x_{D}=4$代入$y=\frac{6}{x}$,得$y_{D}=\frac{3}{2}$,
$\therefore D(4,\frac{3}{2})$.
由$x_{D}=4,x_{A}=1$可知$DH = 3$,
$\therefore\frac{GE}{3}=\frac{1}{3},\therefore GE = 1,\therefore x_{E}=1 + 1 = 2$.
由$y_{A}=6,y_{D}=\frac{3}{2}$可知$AH = 6-\frac{3}{2}=\frac{9}{2}$,
$\therefore\frac{AG}{\frac{9}{2}}=\frac{1}{3},\therefore AG=\frac{3}{2}$,
$\therefore y_{E}=6-\frac{3}{2}=\frac{9}{2},\therefore E(2,\frac{9}{2})$.
②对于$y = 2x + 4$,当$x = 0$时,$y = 4,\therefore C(0,4)$.
$\because CM = 1,\therefore M(0,3)$.
如图
(2),过点 C 作$CP\perp AB$交 AN 于点 P,过点 P 作$PK\perp y$轴于点 K,过点 A 作$AI\perp y$轴于点 I,则$\angle AIC=\angle CKP = 90^{\circ}$.
$\because\angle IAC+\angle ACI = 90^{\circ}=\angle ACI+\angle PCK$,
$\therefore\angle IAC=\angle PCK$.
$\because\angle BAN = 45^{\circ},\triangle ACP$为等腰直角三角形,$\therefore AC = CP$,
$\therefore\triangle IAC\cong\triangle KCP$(AAS)(点拨:“一线三直角”全等模型).
更多讲解详见《解题有招》折页“快招 3”
$\because A(1,6),C(0,4),\therefore CK = AI = 1,PK = CI = 2$.
$\because CM = CK = 1,\therefore$点 M 与点 K 重合,$\therefore P(2,3)$.
设直线 AN 的表达式为$y = k'x + b$,
将$A(1,6),P(2,3)$分别代入,
得$\begin{cases}6 = k'+b,\\3 = 2k'+b,\end{cases}$解得$\begin{cases}k'=-3,\\b = 9,\end{cases}$
$\therefore$直线 AN 的表达式为$y=-3x + 9$.
设$N(m,-3m + 9)$,
$\because$四边形 OMDN 是平行四边形,
$\therefore x_{D}=0 + m-0 = m,y_{D}=3-3m + 9=-3m + 12$,
$\therefore D(m,-3m + 12)$.
$\because D$为反比例函数$y=\frac{6}{x}$图象上的一点,
$\therefore-3m + 12=\frac{6}{m}$,解得$m_{1}=2+\sqrt{2},m_{2}=2-\sqrt{2}$(不合题意,舍去),
$\therefore-3m + 12=-3(2+\sqrt{2})+12=6-3\sqrt{2}$,
$\therefore D(2+\sqrt{2},6-3\sqrt{2})$.