2026年金考卷中考试题汇编45套数学山东专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年金考卷中考试题汇编45套数学山东专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
8. 如图,在三角形纸片ABC中,∠B=57°,∠C=38°,将纸片沿着过点A的直线折叠,使点B落在AC边上的点E处,折痕AD交BC于点D;再将纸片沿着过点E的直线折叠,使点C落在BC边上的点G处,折痕EF交BC于点F.下列结论成立的是(
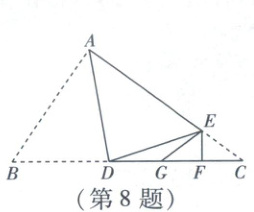
A.DG=EG
B.GE⊥AE
C.∠DAE=42°
D.DE=2GF
A
)
A.DG=EG
B.GE⊥AE
C.∠DAE=42°
D.DE=2GF
答案:
8 A 逐项分析如下,故选A.
选项 分析 正误
A 易知$\angle BAC=85^{\circ}$.由折叠的性质可知$\angle AED=\angle B=57^{\circ},\therefore \angle BDE=360^{\circ}-85^{\circ}-57^{\circ} × 2=161^{\circ},\therefore \angle EDG=180^{\circ}-\angle BDE=180^{\circ}-161^{\circ}=19^{\circ}$.由折叠的性质可知$\angle EGF=\angle C=38^{\circ},\therefore \angle DEG=\angle EGC-\angle EDG=19^{\circ}$(依据:三角形的一个外角等于与它不相邻的两个内角的和)$,\therefore \angle EDG=\angle DEG,\therefore DG=EG$. $\surd$
B $\because \angle AED+\angle DEG=57^{\circ}+19^{\circ}=76^{\circ}$,即$\angle AEG=76^{\circ},\therefore GE$与$AE$不垂直. $×$
C 易知$\angle BAC=85^{\circ}$.由折叠的性质可得$\angle DAE=\angle DAB=\frac{85^{\circ}}{2}=42.5^{\circ}$. $×$
D 如图,过点$G$作$GM \perp DE$于点$M$.假设$DE=2GF$.易知$\angle EFC=\angle EFG=90^{\circ}.\because DG=EG,\therefore \triangle DGE$为等腰三角形.$\because GM \perp DE,\therefore DM=EM$(依据:等腰三角形“三线合一”)$,\therefore DE=2EM,\therefore GF=EM$.在$Rt\triangle EMG$中$,\cos \angle MEG=\frac{EM}{EG},\cos 19^{\circ}=\frac{EM}{EG}$.在$Rt\triangle EFG$中$,\cos \angle EGF=\cos 38^{\circ}=\frac{GF}{EG},\because \cos 19^{\circ} \neq \cos 38^{\circ},\therefore \frac{EM}{EG} \neq \frac{GF}{EG},\therefore EM \neq GF$,与$GF=EM$矛盾$,\therefore DE \neq 2GF$. $×$

8 A 逐项分析如下,故选A.
选项 分析 正误
A 易知$\angle BAC=85^{\circ}$.由折叠的性质可知$\angle AED=\angle B=57^{\circ},\therefore \angle BDE=360^{\circ}-85^{\circ}-57^{\circ} × 2=161^{\circ},\therefore \angle EDG=180^{\circ}-\angle BDE=180^{\circ}-161^{\circ}=19^{\circ}$.由折叠的性质可知$\angle EGF=\angle C=38^{\circ},\therefore \angle DEG=\angle EGC-\angle EDG=19^{\circ}$(依据:三角形的一个外角等于与它不相邻的两个内角的和)$,\therefore \angle EDG=\angle DEG,\therefore DG=EG$. $\surd$
B $\because \angle AED+\angle DEG=57^{\circ}+19^{\circ}=76^{\circ}$,即$\angle AEG=76^{\circ},\therefore GE$与$AE$不垂直. $×$
C 易知$\angle BAC=85^{\circ}$.由折叠的性质可得$\angle DAE=\angle DAB=\frac{85^{\circ}}{2}=42.5^{\circ}$. $×$
D 如图,过点$G$作$GM \perp DE$于点$M$.假设$DE=2GF$.易知$\angle EFC=\angle EFG=90^{\circ}.\because DG=EG,\therefore \triangle DGE$为等腰三角形.$\because GM \perp DE,\therefore DM=EM$(依据:等腰三角形“三线合一”)$,\therefore DE=2EM,\therefore GF=EM$.在$Rt\triangle EMG$中$,\cos \angle MEG=\frac{EM}{EG},\cos 19^{\circ}=\frac{EM}{EG}$.在$Rt\triangle EFG$中$,\cos \angle EGF=\cos 38^{\circ}=\frac{GF}{EG},\because \cos 19^{\circ} \neq \cos 38^{\circ},\therefore \frac{EM}{EG} \neq \frac{GF}{EG},\therefore EM \neq GF$,与$GF=EM$矛盾$,\therefore DE \neq 2GF$. $×$

9. 将二次函数$y=x^{2}-2x-3$的图象在x轴下方的部分以x轴为对称轴翻折到x轴上方,得到如图所示的新函数图象,下列对新函数的描述正确的是(
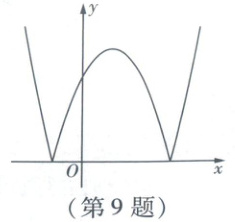
A.图象与y轴的交点坐标是(0,-3)
B.当x=1时,函数取得最大值
C.图象与x轴两个交点之间的距离为4
D.当x>1时,y的值随x值的增大而增大
C
)
A.图象与y轴的交点坐标是(0,-3)
B.当x=1时,函数取得最大值
C.图象与x轴两个交点之间的距离为4
D.当x>1时,y的值随x值的增大而增大
答案:
9 C 逐项分析如下,故选C.
选项 分析 正误
A 对于$y=x^{2}-2x-3$,令$x=0$,则$y=-3,\therefore$二次函数$y=x^{2}-2x-3$的图象与$y$轴的交点坐标为$(0,-3),\therefore$翻折后新函数图象与$y$轴的交点坐标是$(0,3)$. $×$
B 由函数图象可知,该函数没有最大值. $×$
C 对于$y=x^{2}-2x-3$,令$y=0$,则$x^{2}-2x-3=0$,解得$x_{1}=3,x_{2}=-1,\therefore$二次函数$y=x^{2}-2x-3$的图象与$x$轴的交点坐标为$(-1,0),(3,0),\therefore$翻折后新函数图象与$x$轴两个交点之间的距离为$|3-(-1)|=4$. $\surd$
D 易得翻折后新函数图象的对称轴为直线$x=1$,结合函数图象可知,当$1<x<3$时$,y$随$x$的增大而减小;当$x>3$时$,y$随$x$的增大而增大. $×$
选项 分析 正误
A 对于$y=x^{2}-2x-3$,令$x=0$,则$y=-3,\therefore$二次函数$y=x^{2}-2x-3$的图象与$y$轴的交点坐标为$(0,-3),\therefore$翻折后新函数图象与$y$轴的交点坐标是$(0,3)$. $×$
B 由函数图象可知,该函数没有最大值. $×$
C 对于$y=x^{2}-2x-3$,令$y=0$,则$x^{2}-2x-3=0$,解得$x_{1}=3,x_{2}=-1,\therefore$二次函数$y=x^{2}-2x-3$的图象与$x$轴的交点坐标为$(-1,0),(3,0),\therefore$翻折后新函数图象与$x$轴两个交点之间的距离为$|3-(-1)|=4$. $\surd$
D 易得翻折后新函数图象的对称轴为直线$x=1$,结合函数图象可知,当$1<x<3$时$,y$随$x$的增大而减小;当$x>3$时$,y$随$x$的增大而增大. $×$
10. 因式分解:$3x^{2}-3y^{2}=$
$3(x+y)(x-y)$
.
答案:
10 $3(x+y)(x-y)$
11. 为弘扬传统文化、培养学生的劳动意识,某校在端午节期间举行了包粽子活动,每个粽子的标准质量为100g.甲、乙两名同学各包了5个粽子,每个粽子的质量(单位:g)如下:
甲:103,99,100,101,97;
乙:99,103,105,95,98.
甲、乙两名同学包的粽子的质量比较稳定的是
甲:103,99,100,101,97;
乙:99,103,105,95,98.
甲、乙两名同学包的粽子的质量比较稳定的是
甲
(填“甲”或“乙”).
答案:
11 甲
12. 实数a,b在数轴上对应点的位置如图所示,则|a|

<
|b|(填“>”“<”或“=”).
答案:
12 $<$
13. 如图,正八边形ABCDEFGH的顶点A,B,G,H在坐标轴上,顶点C,D,E,F在第一象限.点F在反比例函数$y=\frac{k}{x}(x>0)$的图象上,若AB=$\sqrt{2}$,则k的值为
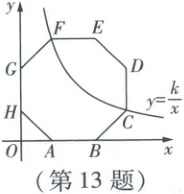
$2+\sqrt{2}$
.
答案:
13 $2+\sqrt{2}$
[解析]如图,过点F作FM⊥y轴于点M.
∵正八边形ABCDEFGH的每个内角的度数为$\frac{(8 - 2) × 180^{\circ}}{8}=135^{\circ}$,$\therefore \angle OHA=\angle OAH=45^{\circ}$.又$\because AH=FG=AB=\sqrt{2}$,$\therefore OH=OA=\frac{\sqrt{2}}{2}AH=1$.同理可得$MG=MF=1$,$\therefore OM=OH+HG+MG=1+\sqrt{2}+1=2+\sqrt{2}$,$\therefore F(1,2+\sqrt{2})$.又$\because$点$F$在反比例函数$y=\frac{k}{x}(x>0)$的图象上$,\therefore k=1 × (2+\sqrt{2})=2+\sqrt{2}$.

13 $2+\sqrt{2}$
[解析]如图,过点F作FM⊥y轴于点M.
∵正八边形ABCDEFGH的每个内角的度数为$\frac{(8 - 2) × 180^{\circ}}{8}=135^{\circ}$,$\therefore \angle OHA=\angle OAH=45^{\circ}$.又$\because AH=FG=AB=\sqrt{2}$,$\therefore OH=OA=\frac{\sqrt{2}}{2}AH=1$.同理可得$MG=MF=1$,$\therefore OM=OH+HG+MG=1+\sqrt{2}+1=2+\sqrt{2}$,$\therefore F(1,2+\sqrt{2})$.又$\because$点$F$在反比例函数$y=\frac{k}{x}(x>0)$的图象上$,\therefore k=1 × (2+\sqrt{2})=2+\sqrt{2}$.

14. 如图,在扇形AOB中,∠AOB=30°,OA=2$\sqrt{3}$,点C在OB上,且OC=AC.延长CB到D,使CD=CA.以CA,CD为邻边作平行四边形ACDE,则图中阴影部分的面积为
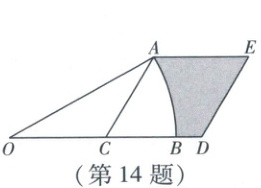
$3\sqrt{3}-\pi$
(结果保留π).
答案:
14 $3\sqrt{3}-\pi$
快招解题法 试题秒解 考场速用
第一步:选定使用方法(分割求和法)
由图可知$,S_{阴影}=S_{\triangle AOC}+S_{正方形ACDE}-S_{扇形OAB}$.
第二步:求涉及的扇形的半径,圆心角;求涉及的三角形的边长、高
如图,过点$A$作$AH \perp OD$于点$H$,则$AH=\frac{1}{2}OA=\sqrt{3}.\because OC=AC,\therefore \angle OAC=\angle AOB=30^{\circ},\therefore \angle ACB=60^{\circ},\therefore AC=2CH$.设$CH=x$,则$AC=2x$.在$Rt\triangle ACH$中,由勾股定理得$x^{2}+(\sqrt{3})^{2}=(2x)^{2}$,解得$x_{1}=1,x_{2}=-1$(舍去)$,\therefore CH=1,AC=2,\therefore CD=CA=OC=2$,
第三步:求阴影部分的面积
$\therefore S_{阴影}=S_{\triangle AOC}+S_{正方形ACDE}-S_{扇形OAB}=\frac{1}{2} × 2 × \sqrt{3}+2 × \sqrt{3}-\frac{30}{360} × \pi × (2\sqrt{3})^{2}=\sqrt{3}+2\sqrt{3}-\pi=3\sqrt{3}-\pi$.

更多讲解详见《解题有招》折页“快招1”
14 $3\sqrt{3}-\pi$
快招解题法 试题秒解 考场速用
第一步:选定使用方法(分割求和法)
由图可知$,S_{阴影}=S_{\triangle AOC}+S_{正方形ACDE}-S_{扇形OAB}$.
第二步:求涉及的扇形的半径,圆心角;求涉及的三角形的边长、高
如图,过点$A$作$AH \perp OD$于点$H$,则$AH=\frac{1}{2}OA=\sqrt{3}.\because OC=AC,\therefore \angle OAC=\angle AOB=30^{\circ},\therefore \angle ACB=60^{\circ},\therefore AC=2CH$.设$CH=x$,则$AC=2x$.在$Rt\triangle ACH$中,由勾股定理得$x^{2}+(\sqrt{3})^{2}=(2x)^{2}$,解得$x_{1}=1,x_{2}=-1$(舍去)$,\therefore CH=1,AC=2,\therefore CD=CA=OC=2$,
第三步:求阴影部分的面积
$\therefore S_{阴影}=S_{\triangle AOC}+S_{正方形ACDE}-S_{扇形OAB}=\frac{1}{2} × 2 × \sqrt{3}+2 × \sqrt{3}-\frac{30}{360} × \pi × (2\sqrt{3})^{2}=\sqrt{3}+2\sqrt{3}-\pi=3\sqrt{3}-\pi$.

更多讲解详见《解题有招》折页“快招1”
15. 如图,在正方形ABCD中,E,F分别为CD,AD的中点.连接BF并延长交AE于点G,交CD的延长线于点M,H为BE的中点,连接GH,CH,CG.下列结论:①CH//AE;②∠M=30°;③$S_{△CGH}=\frac{3}{20}S_{正方形ABCD}$;④AG·MF=CD·AF.其中正确的是
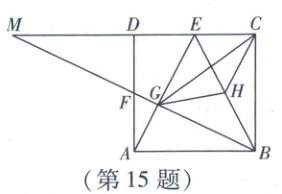
①④
(填写序号).
答案:
15 ①④
[解析]逐项分析如下,故①④正确.
序号 分析 正误
① 易证$\triangle ADE \cong \triangle BCE(SAS),\therefore \angle AED=\angle BEC.\because$在$Rt\triangle BCE$中,点$H$为$BE$的中点$,\therefore HC=\frac{1}{2}BE=HE$(依据:直角三角形斜边上的中线等于斜边的一半)$,\therefore \angle HCE=\angle BEC,\therefore \angle HCE=\angle AED,\therefore CH // AE$. $\surd$
② $\because$四边形$ABCD$是正方形$,\therefore AB // CD$,即$AB // DM,\therefore \angle M=\angle ABF.\because$点$F$为$AD$的中点$,\therefore AF=\frac{1}{2}AD=\frac{1}{2}AB,\therefore \tan M=\tan \angle ABF=\frac{AF}{AB}=\frac{1}{2},\therefore \angle M \neq 30^{\circ}$. $×$
③ $\because CH // AE,\therefore S_{\triangle CGH}=S_{\triangle CEH}$(点拨:同底等高的两个三角形面积相等).设正方形$ABCD$的边长为$2a$,则$S_{正方形ABCD}=(2a)^{2}=4a^{2},\therefore S_{\triangle CEH}=\frac{1}{2}S_{\triangle BCE}=\frac{1}{2} × \frac{1}{2} × 2a × a=\frac{1}{2}a^{2},\therefore S_{\triangle CGH}=\frac{1}{8}S_{正方形ABCD} \neq \frac{3}{20}S_{正方形ABCD}$. $×$
④ 易证$\triangle ADE \cong \triangle BAF(SAS),\therefore \angle EAD=\angle FBA$.又$\because \angle M=\angle FBA,\therefore \angle M=\angle EAD$.易证$\triangle DFM \cong \triangle AFB(AAS),\therefore DM=AB=CD.\because \angle AFG=\angle MFD,\angle M=\angle EAD,\therefore \triangle AFG \sim \triangle MFD,\therefore \frac{AG}{MD}=\frac{AF}{MF}.\because DM=CD,\therefore \frac{AG}{CD}=\frac{AF}{MF},\therefore AG · MF=CD · AF$. $\surd$
[解析]逐项分析如下,故①④正确.
序号 分析 正误
① 易证$\triangle ADE \cong \triangle BCE(SAS),\therefore \angle AED=\angle BEC.\because$在$Rt\triangle BCE$中,点$H$为$BE$的中点$,\therefore HC=\frac{1}{2}BE=HE$(依据:直角三角形斜边上的中线等于斜边的一半)$,\therefore \angle HCE=\angle BEC,\therefore \angle HCE=\angle AED,\therefore CH // AE$. $\surd$
② $\because$四边形$ABCD$是正方形$,\therefore AB // CD$,即$AB // DM,\therefore \angle M=\angle ABF.\because$点$F$为$AD$的中点$,\therefore AF=\frac{1}{2}AD=\frac{1}{2}AB,\therefore \tan M=\tan \angle ABF=\frac{AF}{AB}=\frac{1}{2},\therefore \angle M \neq 30^{\circ}$. $×$
③ $\because CH // AE,\therefore S_{\triangle CGH}=S_{\triangle CEH}$(点拨:同底等高的两个三角形面积相等).设正方形$ABCD$的边长为$2a$,则$S_{正方形ABCD}=(2a)^{2}=4a^{2},\therefore S_{\triangle CEH}=\frac{1}{2}S_{\triangle BCE}=\frac{1}{2} × \frac{1}{2} × 2a × a=\frac{1}{2}a^{2},\therefore S_{\triangle CGH}=\frac{1}{8}S_{正方形ABCD} \neq \frac{3}{20}S_{正方形ABCD}$. $×$
④ 易证$\triangle ADE \cong \triangle BAF(SAS),\therefore \angle EAD=\angle FBA$.又$\because \angle M=\angle FBA,\therefore \angle M=\angle EAD$.易证$\triangle DFM \cong \triangle AFB(AAS),\therefore DM=AB=CD.\because \angle AFG=\angle MFD,\angle M=\angle EAD,\therefore \triangle AFG \sim \triangle MFD,\therefore \frac{AG}{MD}=\frac{AF}{MF}.\because DM=CD,\therefore \frac{AG}{CD}=\frac{AF}{MF},\therefore AG · MF=CD · AF$. $\surd$
查看更多完整答案,请扫码查看


