《2026年金考卷中考试题汇编45套数学山东专版》

9. 下列叙述正确的是(C)

A.顺次连接平行四边形各边中点一定能得到一个矩形
B.平分弦的直径垂直于弦
C.物体在灯泡发出的光照射下形成的影子是中心投影
D.相等的圆心角所对的弧相等，所对的弦相等，所对的弦心距也相等

答案：
19 C 逐项分析如下，故选C。
选项 分析 正误
A 顺次连接平行四边形各边中点不一定能得到一个矩形。例如：如图，四边形$ABCD$是平行四边形（$\angle B\neq90^{\circ}$），顺次连接各边中点，得到四边形$EFGH$。连接$AC$，易得$HG// AC// EF$，$HG = \frac{1}{2}AC = EF$（依据：三角形中位线定理），$\therefore$四边形$EFGH$是平行四边形（依据：一组对边平行且相等的四边形是平行四边形）。故不一定是矩形。
B 平分弦（非直径）的直径垂直于弦。✗
C 依据中心投影的概念可知物体在灯泡发出的光照射下形成的影子是中心投影。✓
D 在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦心距也相等。✗
名师碎碎念：若一束光线是从一点出发的，这样的光线形成的投影称为中心投影，这个点就是中心。

10. 用一个圆心角为 $n^{\circ}$($n$ 为常数，$0 ＜ n ＜ 180$)的扇形作圆锥的侧面，记扇形的半径为 $R$，所作的圆锥的底面圆的周长为 $l$，侧面积为 $S$，当 $R$ 在一定范围内变化时，$l$ 与 $S$ 都随 $R$ 的变化而变化，则 $l$ 与 $R$，$S$ 与 $R$ 满足的函数关系分别是(C)

A.一次函数关系，一次函数关系
B.二次函数关系，二次函数关系
C.一次函数关系，二次函数关系
D.二次函数关系，一次函数关系

答案： 20 C 圆锥的底面圆的周长为$l$，即扇形的弧长$l = \frac{n\pi R}{180} = \frac{n\pi}{180}R$；圆锥的侧面积为$S$，即扇形的面积$S = \frac{n\pi R^{2}}{360} = \frac{n\pi}{360}R^{2}$，所以$l$是$R$的一次函数，$S$是$R$的二次函数。故选C。

11. 若两个相似三角形的相似比是 $1:3$，则这两个相似三角形的面积比是1:9.

答案： 21 $1:9$

12. 因式分解：$(x + 1)(x + 5)+4=$(x+3)^2.

答案： 22 $(x + 3)^{2}$
【解析】原式$= x^{2} + 6x + 5 + 4 = x^{2} + 6x + 9 = (x + 3)^{2}$。

13. 如图，$\triangle ABC$ 中，$\angle B = 30^{\circ}$，将 $\triangle ABC$ 绕点 $C$ 顺时针旋转 $60^{\circ}$ 得到 $\triangle DEC$，点 $A$，$B$ 的对应点分别为 $D$，$E$，延长 $BA$ 交 $DE$ 于点 $F$. 以下结论：① $\angle ACB = \angle ACD$；② $AC// DE$；③ $AB = EF$；④ $BF\perp CE$. 其中正确的结论是④.(填写序号)

答案：
23 ④
【解析】逐个分析如下，故只有结论④正确。
序号 分析 正误
$\because \angle ACB = 60^{\circ} - \angle ACE$，$\angle ACD = 60^{\circ}$，$\angle ACE$不一定等于$0^{\circ}$，$\therefore \angle ACB = \angle ACD$不一定成立。① ✗
$\because \angle ACB$不一定等于$30^{\circ}$，$\therefore \angle ECA$不一定等于$60^{\circ} - 30^{\circ}$，即$\angle ECA$不一定等于$30^{\circ}$，$\therefore \angle E$不一定等于$\angle ECA$，则②$AC// DE$不一定成立。② ✗
③ 将$\triangle ABC$绕点$C$顺时针旋转$60^{\circ}$得到$\triangle DEC$，$\therefore AB = DE = EF + FD$，$\therefore AB$不一定等于$EF$。✗
如图，设$BF$与$CE$交于点$H$。将$\triangle ABC$绕点$C$顺时针旋转$60^{\circ}$得到$\triangle DEC$，$\therefore \angle BCE = \angle ACD = 60^{\circ}$，$\angle E = \angle B = 30^{\circ}$。在$\triangle BHC$中，$\angle BHC = 180^{\circ} - \angle BCE - \angle B = 90^{\circ}$，$\therefore BF\perp CE$。④ ✓

14. 某商场工作人员为方便客户购物需用扶手电梯和直立电梯从一楼运输一批购物车到二楼. 若该商场扶手电梯一次性可以运输 $24$ 辆购物车，直立电梯一次性可以运输 $18$ 辆购物车. 若要运输 $100$ 辆购物车，且最多只能使用电梯 $5$ 次，则共有4种运输方案，分别是使用扶手电梯2次，使用直立电梯3次；使用扶手电梯3次，使用直立电梯2次；使用扶手电梯4次，使用直立电梯1次；使用扶手电梯5次，使用直立电梯0次.

答案： 24 $4$ 使用扶手电梯$2$次，使用直立电梯$3$次；使用扶手电梯$3$次，使用直立电梯$2$次；使用扶手电梯$4$次，使用直立电梯$1$次；使用扶手电梯$5$次，使用直立电梯$0$次
【解析】设使用扶手电梯$x$次，则使用直立电梯$(5 - x)$次。根据题意，得$\begin{cases}24x + 18(5 - x)\geq100\\5 - x\geq0\end{cases}$，解得$\frac{5}{3}\leq x\leq5$。$\because x$为整数，$\therefore x = 2$，$3$，$4$，$5$，故有$4$种方案，即使用扶手电梯$2$次，使用直立电梯$3$次；使用扶手电梯$3$次，使用直立电梯$2$次；使用扶手电梯$4$次，使用直立电梯$1$次；使用扶手电梯$5$次，使用直立电梯$0$次。

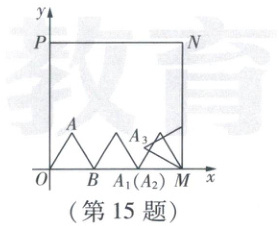
15. 如图，在平面直角坐标系中，正方形 $OMNP$ 的顶点 $M$ 的坐标为 $(3,0)$，$\triangle OAB$ 是等边三角形，点 $B$ 的坐标是 $(1,0)$，$\triangle OAB$ 在正方形 $OMNP$ 内部紧靠正方形 $OMNP$ 的边(方向为 $O\to M\to N\to P\to O\to M\to·s$)做无滑动滚动，第一次滚动后，点 $A$ 的对应点记为 $A_{1}$，$A_{1}$ 的坐标是 $(2,0)$；第二次滚动后，$A_{1}$ 的对应点记为 $A_{2}$，$A_{2}$ 的坐标是 $(2,0)$；第三次滚动后，$A_{2}$ 的对应点记为 $A_{3}$，$A_{3}$ 的坐标是 $(3-\frac{\sqrt{3}}{2},\frac{1}{2})·s·s$则 $A_{2025}$ 的坐标是(\frac{\sqrt{3}}{2},\frac{5}{2}).

答案：
25 $(\frac{\sqrt{3}}{2},\frac{5}{2})$
名师教解题
根据题意，画出$\triangle OAB$在正方形$OMNP$内部紧靠正方形$OMNP$的边（方向为$O\rightarrow M\rightarrow N\rightarrow P\rightarrow O\rightarrow M\rightarrow·s$）做“一个循环”的无滑动滚动，如图所示。

由上图可知，$\triangle OAB$滚动$12$次为一个循环。$\because2025÷12 = 168·s·s9$，$\therefore$点$A_{2025}$的坐标与点$A_9$的坐标相同。易得$\triangle OAB$的高为$\frac{\sqrt{3}}{2}$，点$A_9$的纵坐标为$1 + 1 + \frac{1}{2} = \frac{5}{2}$，$\therefore$点$A_9$的坐标为$(\frac{\sqrt{3}}{2},\frac{5}{2})$，即点$A_{2025}$的坐标为$(\frac{\sqrt{3}}{2},\frac{5}{2})$。
名师讲方法
图形的规律探索题的解题步骤
1. 平面直角坐标系中的规律探索题，一般是求图形上点的坐标，解题步骤如下：
(1)分析图形的变化规律，根据图形的变化规律求出前面几个关键点的坐标；
(2)通过分析变化规律得到一般规律；
(3)按照一般规律写出要求的点的坐标。
2. 图形排列规律探索题的解题步骤：
(1)找到图形之间变与不变的规律；
(2)猜想规律与“序号”间的对应关系，并用关于“序号”的式子表示出来；
(3)验证所归纳的结论，从而进行后续解答。

16. （本题每小题 4 分，共 8 分）
（1）计算：$\vert -3\vert+\sqrt{12}-2\tan 60^{\circ}-(\pi - 2025)^{0}$.
（2）已知关于 $x$ 的分式方程 $\frac{kx}{x - 3}-2=\frac{3}{3 - x}$ 无解，求 $k$ 的值.

答案：
26
(1)原式$= 3 + 2\sqrt{3} - 2\sqrt{3} - 1 = 2$。(2分)
(2)去分母，得$kx - 2(x - 3) = - 3$。
去括号，得$kx - 2x + 6 = - 3$。
移项，得$kx - 2x = - 3 - 6$。
合并同类项，得$(k - 2)x = - 9$。(2分)
当$k - 2 = 0$时，$k = 2$，此时分式方程无解。
当$k - 2\neq0$时，$x = 3$是方程的增根，即$3(k - 2) = - 9$，
解得$k = - 1$。
综上，当$k$的值为$-1$或$2$时，原分式方程无解。(4分)
名师讲方法
解分式方程的步骤