《2025年课堂精练九年级数学上册北师大版四川专版》

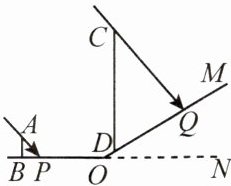
在一个阳光明媚的上午,数学陈老师组织学生测量小山坡上的一棵大树 $CD$ 的高度,山坡 $OM$ 与地面 $ON$ 的夹角为 $30^{\circ}$($\angle MON = 30^{\circ}$),站立在水平地面上身高 1.7 m 的小明 $AB$ 在地面上的影长 $BP$ 为 1.2 m,此刻大树 $CD$ 在斜坡上的影长 $DQ$ 为 5 m,求大树的高度。

答案：
解:如图,过点Q作QE⊥DC于点E,由题意可得△ABP∽△CEQ,则$\frac{AB}{BP}=\frac{EC}{EQ}$,故$\frac{1.7}{1.2}=\frac{EC}{EQ}$.由题意可得EQ//NO,则∠1=∠2=30°.
∵QD=5m,
∴DE=$\frac{5}{2}$m,EQ=$\frac{5\sqrt{3}}{2}$m,故$\frac{1.7}{1.2}=\frac{EC}{EQ}=\frac{EC}{\frac{5\sqrt{3}}{2}}$,解得EC=$\frac{85\sqrt{3}}{24}$,故DE+CE=$\frac{5}{2}+\frac{85\sqrt{3}}{24}=\frac{60+85\sqrt{3}}{24}$ (m),答:大树的高度为$\frac{60+85\sqrt{3}}{24}$m.

某市为了打造森林城市,树立城市新地标,实现绿色、共享发展的理念,在城南建立起了“望月阁”以及环阁公园。小亮、小芳等同学想用一些测量工具和所学的几何知识测量“望月阁”的高度,来检验自己掌握知识和运用知识的能力。他们经过观察发现,观测点与“望月阁”底部的距离不宜测得,因此经过研究需要测量两次,于是他们首先用平面镜进行测量,方法如下：如图,小芳在小亮和“望月阁”之间的直线 $BM$ 上平放一平面镜,在镜面上做了一个标记,这个标记在直线上的对应的位置为点 $C$,镜子不动。小亮看着镜面上的标记,他来回走动,走到点 $D$ 时看到“望月阁”顶端点 $A$ 在镜面中的像与镜面上的标记重合。这时,测得小亮眼睛与地面的高度 $ED = 1.5$ m,$CD = 2$ m。然后在阳光下,他们用测影长的方法进行了第二次测量,方法如下：如图,小亮从点 $D$ 沿 $DM$ 方向走了 16 m,到达“望月阁”影子的末端点 $F$ 处,此时,测得小亮身高 $FG$ 的影长 $FH = 2.5$ m,$FG = 1.65$ m。
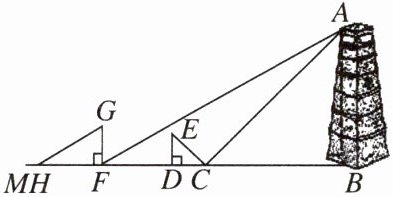
如图,已知 $AB \perp CD$,$ED \perp BM$,$GF \perp BM$,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中提供的相关信息,求出“望月阁”的高 $AB$ 的大小。

答案： 解:由题意得∠ABC=∠EDC=∠GFH=90°,∠ACB=∠ECD,∠AFB=∠GHF,
∴△ABC∽△EDC,△ABF∽△GFH,
∴$\frac{AB}{ED}=\frac{BC}{DC}$,$\frac{AB}{GF}=\frac{BF}{FH}$,则$\frac{AB}{1.5}=\frac{BC}{2}$,$\frac{AB}{1.65}=\frac{BC+18}{2.5}$,所以AB=99m.