第96页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
10. 如图,在圆桌的正上方有一盏吊灯,灯光下,圆桌在地板上的投影是面积为$4\pi\ m^2$的圆. 已知圆桌的高度为$1\ m$,圆桌面的半径为$0.5\ m$,求吊灯到圆桌面的距离.


答案:
解:由题意知,投影的半径CD=2m.由题意得
△PAB∽△PCD,
∴$\frac{PA}{PC}=\frac{AB}{CD}$,
∴$\frac{PA}{PA+1}=\frac{0.5}{2}$,
∴PA=$\frac{1}{3}$m,即吊灯到圆桌面的距离为$\frac{1}{3}$m.
△PAB∽△PCD,
∴$\frac{PA}{PC}=\frac{AB}{CD}$,
∴$\frac{PA}{PA+1}=\frac{0.5}{2}$,
∴PA=$\frac{1}{3}$m,即吊灯到圆桌面的距离为$\frac{1}{3}$m.
11. 如图,墙壁$D$处有一盏灯,小明站在$A处测得他的影长与身长都为1.6\ m$,小明向墙壁走$1\ m到B处发现影子刚好落在A$点,求灯泡与地面的距离$CD$.(结果精确到$0.01\ m$)
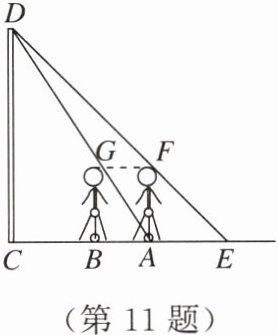

答案:
解:如图,根据题意得BG=AF=AE=1.6m,
AB=1m.
∵BG//AF//CD,
∴△EAF∽△ECD,△ABG∽△ACD,
∴AE∶EC=AF∶CD,AB∶AC=BG∶CD.
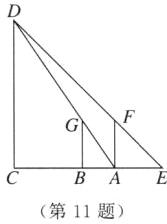
设BC=xm,CD=ym,则CE=(x+2.6)m,
AC=(x+1)m.
∴$\frac{1.6}{x+2.6}=\frac{1.6}{y}$,$\frac{1}{x+1}=\frac{1.6}{y}$,
解得$x=\frac{5}{3}$,$y=\frac{64}{15}$,
∴$CD=\frac{64}{15}m≈4.27m$,
即灯泡与地面的距离约为4.27m.
解:如图,根据题意得BG=AF=AE=1.6m,
AB=1m.
∵BG//AF//CD,
∴△EAF∽△ECD,△ABG∽△ACD,
∴AE∶EC=AF∶CD,AB∶AC=BG∶CD.

设BC=xm,CD=ym,则CE=(x+2.6)m,
AC=(x+1)m.
∴$\frac{1.6}{x+2.6}=\frac{1.6}{y}$,$\frac{1}{x+1}=\frac{1.6}{y}$,
解得$x=\frac{5}{3}$,$y=\frac{64}{15}$,
∴$CD=\frac{64}{15}m≈4.27m$,
即灯泡与地面的距离约为4.27m.
如图,$AB$,$CD$,$EF$是与路灯在同一直线上的三个等高的标杆,相邻的两个标杆之间的距离都是$2\ m$,已知$AB$,$CD在路灯光下的影长分别为BM = 1.6\ m$,$DN = 0.6\ m$,求标杆$EF$的影长.


答案:
解:如图,OH为路灯的高,FG为EF的影长,设
AB=CD=EF=a.
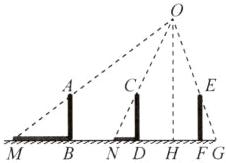
∵AB//OH,
∴△MAB∽△MOH,
∴$\frac{AB}{OH}=\frac{MB}{MH}$,即$\frac{a}{OH}=\frac{1.6}{1.6+2+DH}$①.
∵CD//OH,
∴△NCD∽△NOH,
∴$\frac{CD}{OH}=\frac{ND}{NH}$,即$\frac{a}{OH}=\frac{0.6}{0.6+DH}$②,
由①②得$\frac{0.6}{0.6+DH}=\frac{1.6}{1.6+2+DH}$,
解得DH=1.2,
∴$\frac{a}{OH}=\frac{0.6}{0.6+DH}=\frac{1.6}{1.6+2+DH}=\frac{1}{3}$,
∴HF=DF - DH=2 - 1.2=0.8.
∵EF//OH,
∴△GEF∽△GOH,
∴$\frac{EF}{OH}=\frac{GF}{GH}$,即$\frac{a}{OH}=\frac{FG}{FG+0.8}=\frac{1}{3}$,
∴FG=0.4.
答:标杆EF的影长为0.4m.
解:如图,OH为路灯的高,FG为EF的影长,设
AB=CD=EF=a.

∵AB//OH,
∴△MAB∽△MOH,
∴$\frac{AB}{OH}=\frac{MB}{MH}$,即$\frac{a}{OH}=\frac{1.6}{1.6+2+DH}$①.
∵CD//OH,
∴△NCD∽△NOH,
∴$\frac{CD}{OH}=\frac{ND}{NH}$,即$\frac{a}{OH}=\frac{0.6}{0.6+DH}$②,
由①②得$\frac{0.6}{0.6+DH}=\frac{1.6}{1.6+2+DH}$,
解得DH=1.2,
∴$\frac{a}{OH}=\frac{0.6}{0.6+DH}=\frac{1.6}{1.6+2+DH}=\frac{1}{3}$,
∴HF=DF - DH=2 - 1.2=0.8.
∵EF//OH,
∴△GEF∽△GOH,
∴$\frac{EF}{OH}=\frac{GF}{GH}$,即$\frac{a}{OH}=\frac{FG}{FG+0.8}=\frac{1}{3}$,
∴FG=0.4.
答:标杆EF的影长为0.4m.
如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由$A处径直走到B$处,她在灯光照射下的影长$l与行走的路程s$之间的变化关系用图象表示出来大致是( ).
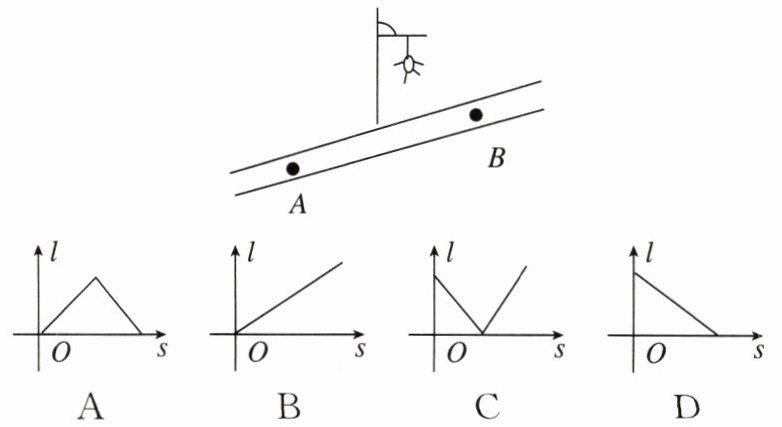

答案:
C
查看更多完整答案,请扫码查看


