《2025年课堂精练九年级数学上册北师大版四川专版》

8. 如图,在菱形 $ABCD$ 中,$AB = 5$,对角线 $AC$ 与 $BD$ 相交于点 $O$,且 $AC:BD = 3:4$,$AE \perp CD$ 于点 $E$,则 $AE$ 的长是______.

答案： $\frac{24}{5}$

9. 如图,将菱形纸片 $ABCD$ 折叠,使点 $A$ 恰好落在菱形的对称中心点 $O$ 处,折痕为 $EF$. 若菱形 $ABCD$ 的边长为 $2\ cm$,$\angle A = 120^{\circ}$,则 $EF = $______.

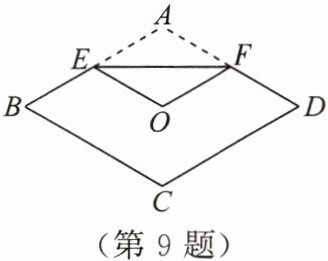
答案： $\sqrt{3}\ cm$

10. 如图,已知四边形 $ABCD$,$ADEF$ 都是菱形,$\angle BAD = \angle FAD$,$\angle BAD$ 为锐角.
(1) 求证：$AD \perp BF$；
(2) 若 $BF = BC$,求 $\angle ADC$ 的度数.

答案：
（1）证明：
∵四边形$ABCD$，$ADEF$都是菱形，
∴$AB=BC=CD=DA$，$AD=DE=EF=FA$，
∴$AB=AF$．
∵$\angle BAD=\angle FAD$，
∴$AD\perp BF$（等腰三角形三线合一）．
（2）解：如图，记$AD\perp BF$于$H$．
∵$AB=AF$，
∴$BH=HF=\frac{1}{2}BF$．
∵$BF=BC$，$AB=BC$，
∴$BF=AB$，
∴$BH=\frac{1}{2}AB$，
∴在$Rt\triangle ABH$中，$\angle BAH=30^{\circ}$．
∵在菱形$ABCD$中，$\angle ADC+\angle BAD=180^{\circ}$，
∴$\angle ADC=180^{\circ}-30^{\circ}=150^{\circ}$．
　　　　　　　　　　　　

如图,在菱形 $ABCD$ 中,对角线 $BD$,$AC$ 的长分别为 $12$ 和 $16$,$E$,$F$ 分别是边 $AB$,$AD$ 的中点,$H$ 是对角线 $BD$ 上任意一点,则 $HE + HF$ 的最小值是______.

答案： 10

小敏思考如何解决如下问题.
原题：如图①,点 $P$,$Q$ 分别在菱形 $ABCD$ 的边 $BC$,$CD$ 上,$\angle PAQ = \angle B$,求证：$AP = AQ$.
(1) 小敏进行探索,若将点 $P$,$Q$ 的位置特殊化：把 $\angle PAQ$ 绕点 $A$ 旋转得到 $\angle EAF$,使 $AE \perp BC$,点 $E$,$F$ 分别在边 $BC$,$CD$ 上,如图②,此时她证明了 $AE = AF$,请你证明.
(2) 受以上(1)的启发,请在图①中添加辅助线,完成原题的证明.
(3) 如果在原题中添加条件：$AB = 4$,$\angle B = 60^{\circ}$,求四边形 $APCQ$ 的面积.

答案：
（1）证明：
∵四边形$ABCD$是菱形，
∴$\angle B+\angle C=180^{\circ}$，$\angle B=\angle D$，$AB=AD$．
∵$\angle EAF=\angle B$，
∴$\angle EAF+\angle C=180^{\circ}$，
∴$\angle AEC+\angle AFC=180^{\circ}$．
∵$AE\perp BC$，
∴$AF\perp CD$．
在$\triangle AEB$和$\triangle AFD$中，
$\begin{cases}\angle AEB=\angle AFD,\\\angle B=\angle D,\\AB=AD,\end{cases}$
∴$\triangle AEB\cong\triangle AFD$，
∴$AE=AF$．
（2）证明：如图，作$AE\perp BC$，$AF\perp CD$，垂足分别为点$E$，$F$．由（1）得，$\angle PAQ=\angle EAF=\angle B$，$AE=AF$，
∴$\angle EAP=\angle FAQ$，
在$\triangle AEP$和$\triangle AFQ$中，
$\begin{cases}\angle AEP=\angle AFQ,\\AE=AF,\\\angle EAP=\angle FAQ,\end{cases}$
∴$\triangle AEP\cong\triangle AFQ$，
∴$AP=AQ$．
（3）解：如图，连接$AC$，$BD$交于$O$，
　　　　　　　　　　　　
∵$\angle ABC=60^{\circ}$，$BA=BC$，
∴$\triangle ABC$为等边三角形．
∵$AE\perp BC$，
∴$BE=EC$，
同理，$CF=FD$，
∴四边形$AECF$的面积$=\frac{1}{2}×$四边形$ABCD$的面积．
由（2）得，四边形$APCQ$的面积$=$四边形$AECF$的面积，$OA=\frac{1}{2}AB=2$，$OB=\sqrt{AB^{2}-OA^{2}}=2\sqrt{3}$，
∴四边形$ABCD$的面积$=\frac{1}{2}×2×2\sqrt{3}×4=8\sqrt{3}$，
∴四边形$APCQ$的面积$=4\sqrt{3}$．