《2025年课堂精练九年级数学上册北师大版四川专版》

9. 已知线段 $ MN $,$ P $ 是它的黄金分割点. 若 $ MN = \sqrt{5} + 1 $,则线段 $ MP $ 的长是 ______.

答案： 2或√5-1

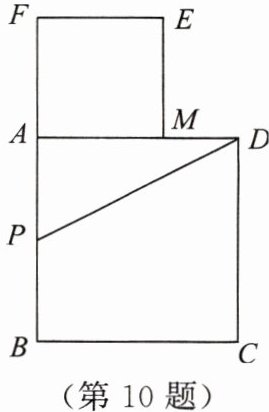
10. 如图,以长为 $ 2 $ 的线段 $ AB $ 为边作正方形 $ ABCD $,取 $ AB $ 的中点 $ P $,连接 $ PD $,在 $ BA $ 的延长线上取点 $ F $,使 $ PF = PD $,以 $ AF $ 为边作正方形 $ AMEF $,点 $ M $ 落在边 $ AD $ 上.
(1) 求 $ AM $,$ DM $ 的长；
(2) 求证：$ AM^2 = AD \cdot DM $；
(3) 根据(2)的结论你能找出图中的黄金分割点吗？
]

答案：
(1)解:
∵正方形ABCD的边长为2,P是AB中点,
∴AB=AD=2,AP=1.在Rt△APD中,PD=√(AP²+AD²)=√5.
∵PF=PD,
∴AF=PF-AP=√5-1.
∵四边形AMEF是正方形,
∴AM=AF=√5-1.
∴DM=AD-AM=2-(√5-1)=3-√5.
(2)证明:由
(1)得AM²=(√5-1)²=6-2√5,AD·DM=2×(3-√5)=6-2√5,
∴AM²=AD·DM.
(3)解:点M是线段AD的黄金分割点.

宽与长的比是 $\frac{\sqrt{5} - 1}{2}$ 的矩形叫黄金矩形. 心理测试表明：黄金矩形令人赏心悦目,它给我们以协调、匀称的美感. 现将某同学在数学活动课中,折叠黄金矩形的方法归纳如下(如图)：
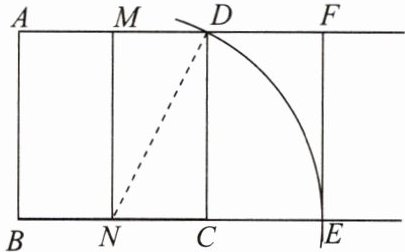
第一步：作一个正方形 $ ABCD $；
第二步：分别取 $ AD $,$ BC $ 的中点 $ M $,$ N $,连接 $ MN $；
第三步：以点 $ N $ 为圆心,$ ND $ 长为半径画弧,交 $ BC $ 的延长线于点 $ E $；
第四步：过点 $ E $ 作 $ EF \perp AD $,交 $ AD $ 的延长线于点 $ F $.
请你根据以上作法,求证：矩形 $ DCEF $ 为黄金矩形.
]

答案： 证明:在正方形ABCD中,设AB=2a.
∵N为BC的中点,
∴NC=1/2BC=a.在Rt△DNC中,ND=√(NC²+CD²)=√(a²+(2a)²)=√5a.又
∵NE=ND,
∴CE=NE-NC=(√5-1)a,
∴CE/CD=((√5-1)a)/(2a)=(√5-1)/2,故矩形DCEF为黄金矩形.

实数 $ a $,$ n $,$ m $,$ b $ 满足 $ a ＜ n ＜ m ＜ b $,这四个数在数轴上对应的点分别为 $ A $,$ N $,$ M $,$ B $(如图). 若 $ AM^2 = BM \cdot AB $,$ BN^2 = AN \cdot AB $,则称 $ m $ 为 $ a $,$ b $ 的“大黄金数”,$ n $ 为 $ a $,$ b $ 的“小黄金数”. 当 $ b - a = 2 $ 时,$ a $,$ b $ 的大黄金数与小黄金数之差 $ m - n = $ ______.
]

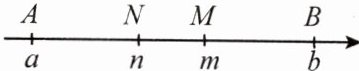
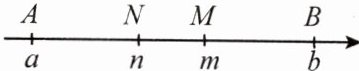
答案： 2√5-4