第24页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
7. 如图,$□ ABCD的对角线AC$,$BD相交于点O$,$AE = CF$。
(1)求证:$\triangle BOE≌\triangle DOF$;
(2)若$BD = EF$,连接$DE$,$BF$,判断四边形$EBFD$的形状,并说明理由。

(1)求证:$\triangle BOE≌\triangle DOF$;
(2)若$BD = EF$,连接$DE$,$BF$,判断四边形$EBFD$的形状,并说明理由。

答案:
(1)证明:
∵四边形ABCD是平行四边形,
∴BO=DO,AO=OC.
∵AE=CF,
∴OE=OF.
在△BOE和△DOF中,
$\left\{\begin{array}{l} OB=OD,\\ ∠BOE=∠DOF,\\ OE=OF,\end{array}\right. $
∴△BOE≌△DOF(SAS).
(2)解:矩形.理由如下:
由
(1)知BO=DO,OE=OF,
∴四边形EBFD是平行四边形.
∵BD=EF,
∴四边形EBFD是矩形.
(1)证明:
∵四边形ABCD是平行四边形,
∴BO=DO,AO=OC.
∵AE=CF,
∴OE=OF.
在△BOE和△DOF中,
$\left\{\begin{array}{l} OB=OD,\\ ∠BOE=∠DOF,\\ OE=OF,\end{array}\right. $
∴△BOE≌△DOF(SAS).
(2)解:矩形.理由如下:
由
(1)知BO=DO,OE=OF,
∴四边形EBFD是平行四边形.
∵BD=EF,
∴四边形EBFD是矩形.
8. 如图,菱形$ABCD的对角线AC和BD相交于点O$,且$BE// AC$,$CE// BD$。
(1)求证:四边形$OBEC$是矩形;
(2)若菱形$ABCD的周长是4\sqrt{10}$,$BD = 2AC$,求四边形$OBEC$的面积。

(1)求证:四边形$OBEC$是矩形;
(2)若菱形$ABCD的周长是4\sqrt{10}$,$BD = 2AC$,求四边形$OBEC$的面积。

答案:
(1)证明:
∵菱形ABCD的对角线AC和BD相交于点O,
∴AC⊥BD.
∵BE//AC,CE//BD,
∴∠BOC=∠OCE=∠OBE=90°,
∴四边形OBEC是矩形.
(2)解:
∵菱形ABCD的周长是$4\sqrt {10}$,
∴AB=BC=AD=DC=$\sqrt {10}$.
∵BD=2AC,
∴BO=2CO.
设CO=x,则BO=2x,
∴$x^{2}+(2x)^{2}=(\sqrt {10})^{2}$,解得$x=\sqrt {2}$,
即$CO=\sqrt {2}$,
∴$BO=2\sqrt {2}$,
∴四边形OBEC的面积为$\sqrt {2}×2\sqrt {2}=4$.
(1)证明:
∵菱形ABCD的对角线AC和BD相交于点O,
∴AC⊥BD.
∵BE//AC,CE//BD,
∴∠BOC=∠OCE=∠OBE=90°,
∴四边形OBEC是矩形.
(2)解:
∵菱形ABCD的周长是$4\sqrt {10}$,
∴AB=BC=AD=DC=$\sqrt {10}$.
∵BD=2AC,
∴BO=2CO.
设CO=x,则BO=2x,
∴$x^{2}+(2x)^{2}=(\sqrt {10})^{2}$,解得$x=\sqrt {2}$,
即$CO=\sqrt {2}$,
∴$BO=2\sqrt {2}$,
∴四边形OBEC的面积为$\sqrt {2}×2\sqrt {2}=4$.
9. 如图,在矩形$ABCD$中,$AD = 6$,$DC = 8$,菱形$EFGH的三个顶点E$,$G$,$H分别在矩形ABCD的边AB$,$CD$,$DA$上,$AH = 2$,连接$CF$。
(1)若$DG = 2$,求证:四边形$EFGH$为正方形;
(2)若$DG = 6$,求$\triangle FCG$的面积。

(1)若$DG = 2$,求证:四边形$EFGH$为正方形;
(2)若$DG = 6$,求$\triangle FCG$的面积。

答案:
(1)证明:
∵四边形EFGH是菱形,
∴HG=EH.
∵AH=2,DG=2,
∴DG=AH.
在Rt△DHG和△AEH中,
$\left\{\begin{array}{l} HG=EH,\\ DG=AH,\end{array}\right. $
∴Rt△DHG≌Rt△AEH,
∴∠DHG=∠AEH.
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°.
∵四边形EFGH为菱形,
∴四边形EFGH为正方形.
(2)解:如图,作FQ⊥CD交DC的延长线于Q,连接GE.
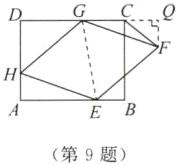
∵四边形ABCD为矩形,
∴AB//CD,
∴∠AEG=∠QGE,
即∠AEH+∠HEG=∠QGF+∠FGE.
∵四边形EFGH为菱形,
∴HE=GF,HE//GF,
∴∠HEG=∠FGE,
∴∠AEH=∠QGF.
在△AEH和△QGF中,
$\left\{\begin{array}{l} ∠A=∠Q,\\ ∠AEH=∠QGF,\\ HE=FG,\end{array}\right. $
∴△AEH≌△QGF,
∴AH=QF=2.
∵DG=6,CD=8,
∴CG=2,
∴△FCG的面积=$\frac {1}{2}CG\cdot FQ=\frac {1}{2}×2×2=2$.
(1)证明:
∵四边形EFGH是菱形,
∴HG=EH.
∵AH=2,DG=2,
∴DG=AH.
在Rt△DHG和△AEH中,
$\left\{\begin{array}{l} HG=EH,\\ DG=AH,\end{array}\right. $
∴Rt△DHG≌Rt△AEH,
∴∠DHG=∠AEH.
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°.
∵四边形EFGH为菱形,
∴四边形EFGH为正方形.
(2)解:如图,作FQ⊥CD交DC的延长线于Q,连接GE.

∵四边形ABCD为矩形,
∴AB//CD,
∴∠AEG=∠QGE,
即∠AEH+∠HEG=∠QGF+∠FGE.
∵四边形EFGH为菱形,
∴HE=GF,HE//GF,
∴∠HEG=∠FGE,
∴∠AEH=∠QGF.
在△AEH和△QGF中,
$\left\{\begin{array}{l} ∠A=∠Q,\\ ∠AEH=∠QGF,\\ HE=FG,\end{array}\right. $
∴△AEH≌△QGF,
∴AH=QF=2.
∵DG=6,CD=8,
∴CG=2,
∴△FCG的面积=$\frac {1}{2}CG\cdot FQ=\frac {1}{2}×2×2=2$.
10. 如图,在正方形$ABCD$中,$AB = 4$,点$E是对角线AC$上的一点,连接$DE$。过点$E作EF⊥ED$,交$AB于点F$,以$DE$,$EF为邻边作矩形GFED$,连接$AG$。
(1)求证:矩形$GFED$是正方形;
(2)求$AG + AE$的值。
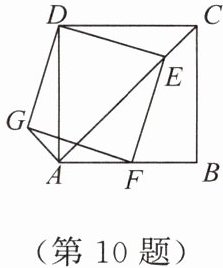
(1)求证:矩形$GFED$是正方形;
(2)求$AG + AE$的值。

答案:
(1)证明:如图,作EM⊥AD于M,EN⊥AB于N.

∵四边形ABCD是正方形,
∴∠EAD=∠EAB.
∵EM⊥AD于M,EN⊥AB于N,
∴EM=EN.
∵∠EMA=∠ENA=∠DAB=90°,
∴四边形ANEM是矩形,
∴∠MEN=∠DEF=90°.
∴∠DEM=∠FEN.
∵∠EMD=∠ENF=90°,EM=EN,
∴△EMD≌△ENF,
∴ED=EF.
∵四边形GFED是矩形,
∴四边形GFED是正方形.
(2)解:
∵四边形GFED是正方形,四边形ABCD是正方形,
∴DG=DE,DC=DA=AB=4,∠GDE=∠ADC=90°,
∴∠ADG=∠CDE,
∴△ADG≌△CDE,
∴AG=CE,
∴AG+AE=EC+AE=AC=$\sqrt {2}AD=4\sqrt {2}$.
(1)证明:如图,作EM⊥AD于M,EN⊥AB于N.

∵四边形ABCD是正方形,
∴∠EAD=∠EAB.
∵EM⊥AD于M,EN⊥AB于N,
∴EM=EN.
∵∠EMA=∠ENA=∠DAB=90°,
∴四边形ANEM是矩形,
∴∠MEN=∠DEF=90°.
∴∠DEM=∠FEN.
∵∠EMD=∠ENF=90°,EM=EN,
∴△EMD≌△ENF,
∴ED=EF.
∵四边形GFED是矩形,
∴四边形GFED是正方形.
(2)解:
∵四边形GFED是正方形,四边形ABCD是正方形,
∴DG=DE,DC=DA=AB=4,∠GDE=∠ADC=90°,
∴∠ADG=∠CDE,
∴△ADG≌△CDE,
∴AG=CE,
∴AG+AE=EC+AE=AC=$\sqrt {2}AD=4\sqrt {2}$.
查看更多完整答案,请扫码查看


