《2025年课堂精练九年级数学上册北师大版四川专版》

利用一元二次方程解决实际问题时应注意：当一元二次方程有两个根时,虽然这些根都满足所列的一元二次方程,但未必符合______,因此利用一元二次方程解决实际问题时,一定要将最后结果进行______。

答案： 实际 检验

1. 把一块长 $80$ cm、宽 $60$ cm 的矩形铁皮,在四个角上截去四个相同的小正方形,然后做成底面积为 $1500$ cm^2 的无盖长方体盒子。设小正方形的边长为 $x$ cm,则可列出方程为( )。

A.$x^{2}-70x + 825 = 0$
B.$x^{2}+70x - 825 = 0$
C.$x^{2}-70x - 825 = 0$
D.$x^{2}+70x + 825 = 0$

答案： A

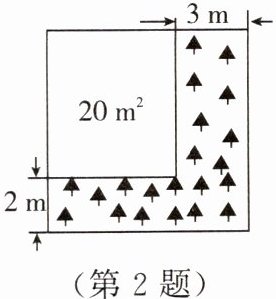
2. 如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了 $2$ m,与其相邻的另一边减少了 $3$ m,剩余一块面积为 $20$ m^2 的矩形空地,则原正方形空地的边长是( )。


A.$7$ m
B.$8$ m
C.$9$ m
D.$10$ m

答案： A

3. 一个软件群里有若干个好友,每个好友都分别给群里其他好友发送一条消息,这样共有 $870$ 条消息,则这个软件群里的好友个数为______。

答案： 30

4. 某市体委要组织一次篮球赛,赛制为单循环形式(每两队之间都赛一场),计划安排 $28$ 场比赛,应邀请多少支球队参加比赛？学习以下解答过程,并完成填空。
解：设应邀请 $x$ 支球队参加比赛,则每队共打______场比赛,比赛总场数用代数式表示为______,根据题意,可列出方程为______,整理得______,解这个方程,得______；经检验,符合实际的解为______。
答：应邀请______支球队参加比赛。

答案： $(x-1)$ $\frac{(x-1)x}{2}$ $\frac{(x-1)x}{2}=28$ $x^{2}-x-56=0$ $x_{1}=8,x_{2}=-7$ $x=8$ 8

5. 两个正方形的面积和为 $106$ cm^2,它们的周长差是 $16$ cm,求这两个正方形的边长分别为多少厘米。

答案： 解:设较小正方形的周长为$x\ cm$,则较大正方形的周长为$(x+16)cm$.由题意列方程:$(\frac{x}{4})^{2}+(\frac{x+16}{4})^{2}=106$,解得$x_{1}=20,x_{2}=-36$(不符合题意,舍去),所以这两个正方形的边长分别为$5\ cm$,$9\ cm$.