《2025年课堂精练九年级数学上册北师大版四川专版》

7. 小刚身高1.7m,测得他站立在阳光下的影子长为0.85m,紧接着他把手臂竖直举起,测得影子长为1.1m,那么小刚举起的手臂超出头顶( ).

A.0.5m
B.0.55m
C.0.6m
D.2.2m

答案： A

8. 如图,数学兴趣小组的小颖想测量教学楼前的一棵树的高,下午课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),她先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是( ).


A.3.25m
B.4.25m
C.4.45m
D.4.75m

答案： C

9. 如图,某班上体育课,甲、乙两名同学分别站在点C,D的位置时,乙影子的顶端恰好与甲影子的顶端A重合. 已知甲身高1.8m,乙身高1.5m,甲的影长是6m,则甲、乙同学相距____.

答案： 1 m

10. 如图,某超市在一楼至二楼之间安装有电梯,天花板与地面平行,张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好完全通过,则两层楼之间的高约为____.

答案： 5.5 m

11. 一天晚上,李明和张龙利用灯光下的影子长来测量一路灯D的高度. 如图,当李明走到点A处时,张龙测得李明直立身高AM与其影子长AE正好相等,接着李明沿AC方向继续向前走,走到点B处时,李明直立身高BN的影子恰好是线段AB,并测得AB= 1.25m. 已知李明直立时的身高为1.75m,求路灯的高CD的长. (结果精确到0.1m)

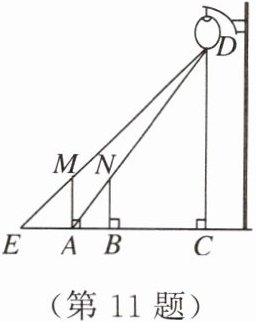
答案： 解:设 CD 的长为 x m,
∵AM⊥EC,CD⊥EC,BN⊥EC,EA=MA,
∴AM//CD,BN//CD,
∴EC=CD=x m,
∴△ABN∽△ACD,
∴$\frac{BN}{CD}=\frac{AB}{AC}$,即$\frac{1.75}{x}=\frac{1.25}{x-1.75}$,
解得 x=6.125≈6.1,
∴路灯的高 CD 的长约为 6.1 m.