《2025年课堂精练九年级数学上册北师大版四川专版》

如图,在△ABC中,O是边AC上一个动点,过点O作直线MN//BC,设MN交∠BCA的平分线于点E,交与∠BCA相邻的△ABC的外角平分线于点F.
(1)判断OE与OF是否相等,并证明你的结论；
(2)判断当点O运动到何处时,四边形AECF为矩形,并证明你的结论.

答案： 解:（1）$OE=OF$.证明如下：
$\because MN// BC$，$CE$平分$\angle ACB$，$CF$平分$\angle ACD$，
$\therefore \angle BCE=\angle ACE=\angle OEC$，
$\angle OCF=\angle FCD=\angle OFC$，
$\therefore OE=OC$，$OC=OF$，$\therefore OE=OF$.
（2）当点$O$运动到$AC$中点时，四边形$AECF$是矩形.证明如下：
$\because AO=CO$，$OE=OF$，
$\therefore$四边形$AECF$是平行四边形.
$\because \angle ECF=\angle ECA+\angle ACF=\frac{1}{2}\angle BCD$，
$\therefore \angle ECF=90^{\circ}$，
$\therefore$四边形$AECF$是矩形.

阅读下面材料.
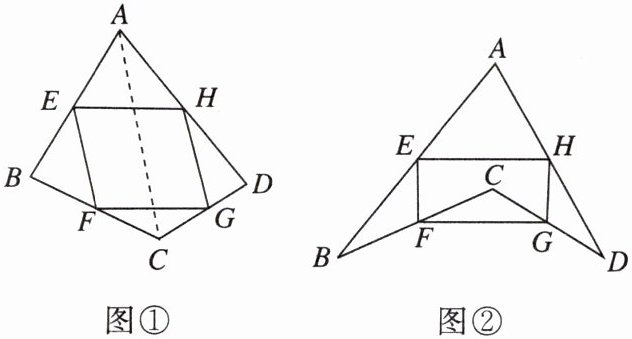
在数学课上,老师请同学们思考如下问题：如图①,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗？
小敏在思考问题时,有如下思路：连接AC.
$\boxed{点E,F分别是AB,BC的中点}\xrightarrow{三角形中线定理}\boxed{\begin{array}{l}EF//AC,\\EF= \frac{1}{2}AC\end{array} }$

$\boxed{点G,H分别是CD,AD的中点}\xrightarrow{三角形中线定理}\boxed{\begin{array}{l}GH//AC,\\GH= \frac{1}{2}AC\end{array} }$
$\to\boxed{\begin{array}{l}EF//GH,\\EF= GH\end{array} }\to\boxed{四边形EFGH是平行四边形}$
结合小敏的思路作答：
(1)若只改变图①中四边形ABCD的形状(如图②),则四边形EFGH还是平行四边形吗？请说明理由.
(2)如图②,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形？写出结论并证明.
②当AC与BD满足什么条件时,四边形EFGH是矩形？直接写出结论.

答案： 解:（1）四边形$EFGH$是平行四边形.理由如下：
连接$AC$（图略）.
$\because E$，$F$分别是$AB$，$BC$的中点，
$\therefore EF// AC$，$EF=\frac{1}{2}AC$.
$\because G$，$H$分别是$CD$，$AD$的中点，
$\therefore GH// AC$，$GH=\frac{1}{2}AC$，
$\therefore EF// GH$，$EF=GH$，
$\therefore$四边形$EFGH$是平行四边形.
（2）①当$AC=BD$时，四边形$EFGH$是菱形.
理由如下：由（1）可知四边形$EFGH$是平行四边形，
当$AC=BD$时，$FG=\frac{1}{2}BD$，$EF=\frac{1}{2}AC$，
$\therefore FG=EF$，
$\therefore$四边形$EFGH$是菱形.
②当$AC\perp BD$时，四边形$EFGH$是矩形.