第77页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
9. 如图,在$\triangle ABC$中,$AB = AC = 10$,延长$AC到点E$,使$CE = AC$,过点$B作BE的垂线交AC于点D$. 若点$D是AC$的中点,则$BE$的长为____.


答案:
$6\sqrt{5}$
10. 如图,$\triangle ABC的顶点A是线段PQ$的中点,$PQ// BC$,连接$PC$,$QB$,分别交$AB$,$AC于点M$,$N$,连接$MN$. 若$MN = 1$,$BC = 3$,则线段$PQ = $____.


答案:
3
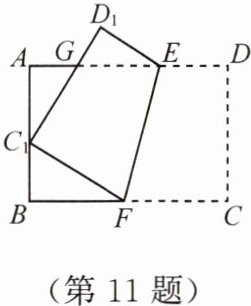
11. 如图,将矩形$ABCD沿EF$折叠,使顶点$C恰好落在AB边的C_1$处,点$D落在点D_1$处,$C_1D_1交线段AE于点G$.
(1)求证:$\triangle BC_1F\backsim\triangle AGC_1$;
(2)若$C_1是AB$的中点,$AB = 6$,$BC = 9$,求$AG$的长.
(1)求证:$\triangle BC_1F\backsim\triangle AGC_1$;
(2)若$C_1是AB$的中点,$AB = 6$,$BC = 9$,求$AG$的长.

答案:
(1)证明:由题意可知$∠A=∠B=∠GC_{1}F=90^{\circ },\therefore ∠BFC_{1}+∠BC_{1}F=90^{\circ },∠AC_{1}G+∠BC_{1}F=90^{\circ },$$\therefore ∠BFC_{1}=∠AC_{1}G,\therefore △BC_{1}F\backsim △AGC_{1}.$
(2)解:$\because C_{1}$是AB的中点,$AB=6,$$\therefore AC_{1}=BC_{1}=3.$$\because ∠B=90^{\circ },\therefore BF^{2}+3^{2}=(9-BF)^{2},\therefore BF=4.$由
(1)得$△AGC_{1}\backsim △BC_{1}F,$$\therefore \frac {AG}{BC_{1}}=\frac {AC_{1}}{BF},\therefore \frac {AG}{3}=\frac {3}{4}$,解得$AG=\frac {9}{4}.$
(1)证明:由题意可知$∠A=∠B=∠GC_{1}F=90^{\circ },\therefore ∠BFC_{1}+∠BC_{1}F=90^{\circ },∠AC_{1}G+∠BC_{1}F=90^{\circ },$$\therefore ∠BFC_{1}=∠AC_{1}G,\therefore △BC_{1}F\backsim △AGC_{1}.$
(2)解:$\because C_{1}$是AB的中点,$AB=6,$$\therefore AC_{1}=BC_{1}=3.$$\because ∠B=90^{\circ },\therefore BF^{2}+3^{2}=(9-BF)^{2},\therefore BF=4.$由
(1)得$△AGC_{1}\backsim △BC_{1}F,$$\therefore \frac {AG}{BC_{1}}=\frac {AC_{1}}{BF},\therefore \frac {AG}{3}=\frac {3}{4}$,解得$AG=\frac {9}{4}.$
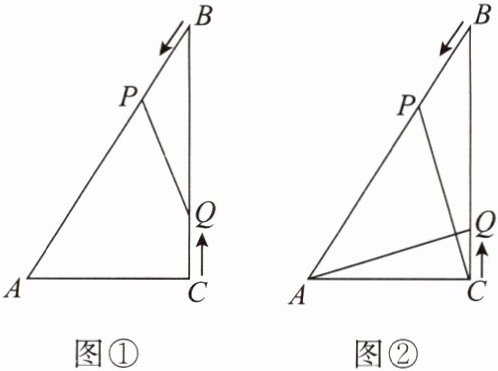
如图①,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = 6\ cm$,$BC = 8\ cm$,动点$P从点B$出发,在$BA边上以5\ cm/s的速度向点A$匀速运动,同时动点$Q从点C$出发,在$CB边上以4\ cm/s的速度向点B$匀速运动,运动时间为$t\ s(0 < t < 2)$,连接$PQ$.
(1)若$\triangle BPQ与\triangle ABC$相似,求$t$的值;
(2)如图②,连接$AQ$,$CP$,若$AQ\perp CP$,求$t$的值;
(3)试证明:$PQ的中点在\triangle ABC$的一条中位线上.
(1)若$\triangle BPQ与\triangle ABC$相似,求$t$的值;
(2)如图②,连接$AQ$,$CP$,若$AQ\perp CP$,求$t$的值;
(3)试证明:$PQ的中点在\triangle ABC$的一条中位线上.

答案:
(1)解:①当$△BPQ\backsim △BAC$时,$\because \frac {BP}{BA}=\frac {BQ}{BC},BP=5tcm,QC=4tcm,AB=$$\sqrt {AC^{2}+BC^{2}}=10cm,BC=8cm,\therefore \frac {5t}{10}=\frac {8-4t}{8},$$\therefore t=1.$②当$△BPQ\backsim △BCA$时,$\because \frac {BP}{BC}=\frac {BQ}{BA}$,即$\frac {5t}{8}=\frac {8-4t}{10},\therefore t=\frac {32}{41},$$\therefore t=1$或$\frac {32}{41}$时,$△BPQ$与$△ABC$相似.
(2)解:如图①,过点P作$PM⊥BC$于点M,AQ,CP交于点N,则有$PB=5tcm,PM=3tcm,$$MC=(8-4t)cm,$$\because ∠NAC+∠NCA=90^{\circ },$$∠PCM+∠NCA=90^{\circ },$$\therefore ∠NAC=∠PCM$且$∠ACQ=∠PMC=90^{\circ },$$\therefore △ACQ\backsim △CMP,$$\therefore \frac {AC}{CM}=\frac {CQ}{MP}$,即$\frac {6}{8-4t}=\frac {4t}{3t},$解得$t=\frac {7}{8}.$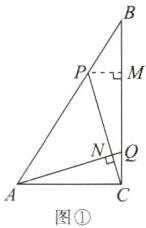
(3)证明:如图②,仍有$PM⊥BC$于点M,PQ的中点设为D点,再作$PE⊥AC$于点E,$DF⊥AC$于点F,$\because ∠ACB=90^{\circ },$$\therefore DF$为梯形PECQ的中位线,$\therefore DF=\frac {PE+QC}{2}.$$\because QC=4tcm,PE=8-BM=(8-4t)cm,$$\therefore DF=\frac {8-4t+4t}{2}=4(cm).$$\because BC=8cm$,过BC的中点R作直线平行于AC,$\therefore RC=DF=4cm$成立,$\therefore D$在过R的中位线上,$\therefore PQ$的中点在$△ABC$的一条中位线上.
(1)解:①当$△BPQ\backsim △BAC$时,$\because \frac {BP}{BA}=\frac {BQ}{BC},BP=5tcm,QC=4tcm,AB=$$\sqrt {AC^{2}+BC^{2}}=10cm,BC=8cm,\therefore \frac {5t}{10}=\frac {8-4t}{8},$$\therefore t=1.$②当$△BPQ\backsim △BCA$时,$\because \frac {BP}{BC}=\frac {BQ}{BA}$,即$\frac {5t}{8}=\frac {8-4t}{10},\therefore t=\frac {32}{41},$$\therefore t=1$或$\frac {32}{41}$时,$△BPQ$与$△ABC$相似.
(2)解:如图①,过点P作$PM⊥BC$于点M,AQ,CP交于点N,则有$PB=5tcm,PM=3tcm,$$MC=(8-4t)cm,$$\because ∠NAC+∠NCA=90^{\circ },$$∠PCM+∠NCA=90^{\circ },$$\therefore ∠NAC=∠PCM$且$∠ACQ=∠PMC=90^{\circ },$$\therefore △ACQ\backsim △CMP,$$\therefore \frac {AC}{CM}=\frac {CQ}{MP}$,即$\frac {6}{8-4t}=\frac {4t}{3t},$解得$t=\frac {7}{8}.$

(3)证明:如图②,仍有$PM⊥BC$于点M,PQ的中点设为D点,再作$PE⊥AC$于点E,$DF⊥AC$于点F,$\because ∠ACB=90^{\circ },$$\therefore DF$为梯形PECQ的中位线,$\therefore DF=\frac {PE+QC}{2}.$$\because QC=4tcm,PE=8-BM=(8-4t)cm,$$\therefore DF=\frac {8-4t+4t}{2}=4(cm).$$\because BC=8cm$,过BC的中点R作直线平行于AC,$\therefore RC=DF=4cm$成立,$\therefore D$在过R的中位线上,$\therefore PQ$的中点在$△ABC$的一条中位线上.

如图,在正方形$ABCD$中,点$E$,$F分别是边AD$,$BC$的中点,连接$DF$,过点$E作EH\perp DF$,垂足为$H$,$EH的延长线交DC于点G$.
(1)猜想$DG与CF$的数量关系,并证明你的结论;
(2)过点$H作MN// CD$,分别交$AD$,$BC于点M$,$N$,若正方形$ABCD的边长为10$,点$P是MN$上一点,求$\triangle PDC$周长的最小值.

(1)猜想$DG与CF$的数量关系,并证明你的结论;
(2)过点$H作MN// CD$,分别交$AD$,$BC于点M$,$N$,若正方形$ABCD的边长为10$,点$P是MN$上一点,求$\triangle PDC$周长的最小值.

答案:
解:
(1)$CF=2DG$.证明如下:
∵四边形ABCD是正方形,$\therefore AD=BC=CD=AB,∠ADC=∠C=90^{\circ }.$$\because DE=AE,\therefore AD=CD=2DE.$$\because EG⊥DF,\therefore ∠DHG=90^{\circ },$$\therefore ∠CDF+∠DGE=90^{\circ },∠DGE+∠DEG=90^{\circ },$$\therefore ∠CDF=∠DEG,\therefore △DEG\backsim △CDF,$$\therefore \frac {DG}{CF}=\frac {DE}{DC}=\frac {1}{2},\therefore CF=2DG.$
(2)如图,作点C关于NM的对称点K,连接DK交MN于点P,连接PC,此时$△PDC$的周长最短.周长的最小值$=CD+PD+PC=CD+PD+PK=CD+DK.$由题意得$CD=AD=10,DE=AE=5,DG=\frac {5}{2},$$EG=\frac {5}{2}\sqrt{5},DH=\frac {DE\cdot DG}{EG}=\sqrt {5},$$\therefore EH=\sqrt {DE^{2}-DH^{2}}=2\sqrt {5},$$\therefore HM=\frac {DH\cdot EH}{DE}=2,$$\therefore DM=CN=NK=\sqrt {DH^{2}-HM^{2}}=1.$ 在$Rt△DCK$中,$DK=\sqrt {CD^{2}+CK^{2}}=\sqrt {10^{2}+2^{2}}=2\sqrt {26},$$\therefore △PCD$的周长的最小值为$10+2\sqrt {26}.$
在$Rt△DCK$中,$DK=\sqrt {CD^{2}+CK^{2}}=\sqrt {10^{2}+2^{2}}=2\sqrt {26},$$\therefore △PCD$的周长的最小值为$10+2\sqrt {26}.$
解:
(1)$CF=2DG$.证明如下:
∵四边形ABCD是正方形,$\therefore AD=BC=CD=AB,∠ADC=∠C=90^{\circ }.$$\because DE=AE,\therefore AD=CD=2DE.$$\because EG⊥DF,\therefore ∠DHG=90^{\circ },$$\therefore ∠CDF+∠DGE=90^{\circ },∠DGE+∠DEG=90^{\circ },$$\therefore ∠CDF=∠DEG,\therefore △DEG\backsim △CDF,$$\therefore \frac {DG}{CF}=\frac {DE}{DC}=\frac {1}{2},\therefore CF=2DG.$
(2)如图,作点C关于NM的对称点K,连接DK交MN于点P,连接PC,此时$△PDC$的周长最短.周长的最小值$=CD+PD+PC=CD+PD+PK=CD+DK.$由题意得$CD=AD=10,DE=AE=5,DG=\frac {5}{2},$$EG=\frac {5}{2}\sqrt{5},DH=\frac {DE\cdot DG}{EG}=\sqrt {5},$$\therefore EH=\sqrt {DE^{2}-DH^{2}}=2\sqrt {5},$$\therefore HM=\frac {DH\cdot EH}{DE}=2,$$\therefore DM=CN=NK=\sqrt {DH^{2}-HM^{2}}=1.$
 在$Rt△DCK$中,$DK=\sqrt {CD^{2}+CK^{2}}=\sqrt {10^{2}+2^{2}}=2\sqrt {26},$$\therefore △PCD$的周长的最小值为$10+2\sqrt {26}.$
在$Rt△DCK$中,$DK=\sqrt {CD^{2}+CK^{2}}=\sqrt {10^{2}+2^{2}}=2\sqrt {26},$$\therefore △PCD$的周长的最小值为$10+2\sqrt {26}.$ 查看更多完整答案,请扫码查看


