《2025年课堂精练九年级数学上册北师大版四川专版》

7. 晚上小辉到广场去玩,他发现有两人的影子一个向东,一个向西,于是他肯定地说：“广场上的大灯泡一定位于两人______. ”

答案： 中间上方

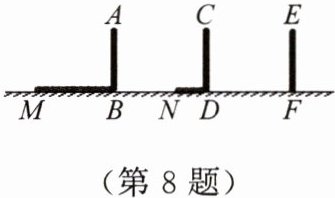
8. 如图,电线杆上有一盏路灯$O$,电线杆与三个等高的标杆整齐划一地排列在马路的一侧,$AB$,$CD$,$EF$是三个标杆.
(1)请画出路灯$O$的位置；
(2)画出标杆$EF在路灯下的影子FH$.

答案：
解：
(1)如图，点O为所作.
(2)如图，FH为所作.

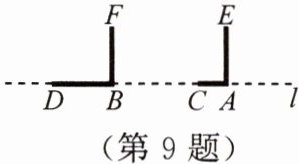
9. 高高的路灯挂在路边的上方,高傲而明亮,小明拿着一根$2\ m$长的竹竿,想量一量路灯的高度,直接量是不可能的. 于是,他走到路灯旁的一个地方,竖起竹竿(即$AE$),这时,他量了一下竹竿的影长(即$AC$)正好是$1\ m$,他沿着影子的方向走,向远处走出两根竹竿的长度(即$AB = 4\ m$),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即$BD = 2\ m$). 此时,小明抬头瞧瞧路灯,若有所思地说：“噢,我知道路灯有多高了！”同学们,请你和小明一起解答这个问题：
(1)在图中作出路灯$O$的位置,并作$OP\perp l于P$；
(2)求出路灯$O$的高度,并说明理由.

答案：
解：
(1)如图所示.

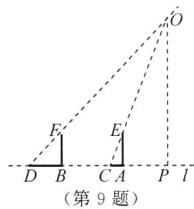
(2)
∵BF=DB=2m，即∠D=45°，
∴DP=OP=灯高.
在△COP中，AE⊥CP，OP⊥CP，
∴AE//OP，
∴△CEA∽△COP，即$\frac{CA}{EA}=\frac{CP}{OP}$.
设AP=x，OP=h，则$\frac{1}{2}=\frac{1+x}{h}$①，
DP=OP，则2+4+x=h②，
联立①②两式得x=4，h=10，
∴路灯有10m高.