第19页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
7. 如图,已知 $E$ 是正方形 $ABCD$ 的对角线 $AC$ 上一点,$AE = AD$,过点 $E$ 作 $AC$ 的垂线,交边 $CD$ 于点 $F$,那么 $\angle FAD= $____。


答案:
22.5°
8. 如图,正方形 $ABCD$ 的边长为 $1$,以对角线 $AC$ 为边作第 $2$ 个正方形,再以对角线 $AE$ 为边作第 $3$ 个正方形……如此下去,第 $n$ 个正方形的边长为____。
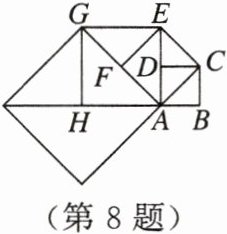

答案:
$(\sqrt{2})^{n-1}$
9. 如图,小明把两个大小完全一样的正方形放置在一起,他发现正方形 $A'B'C'O$ 绕点 $O$ 无论怎样转动,两个正方形重叠部分的面积总等于一个正方形面积的 $\frac{1}{4}$,请你说明其中的理由。


答案:
解:
∵四边形ABCD为正方形,
∴∠OAE=∠OBF=45°,BO⊥AC,即∠AOE+∠EOB=90°.又
∵四边形A'B'C'O为正方形,
∴∠A'OC'=90°,即∠BOE+∠BOC'=90°,
∴∠AOE=∠BOF.在△AOE和△BOF中,$\left\{\begin{array}{l}∠AOE=∠BOF,\\AO=BO,\\∠OAE=∠OBF,\end{array}\right.$
∴△AOE≌△BOF(ASA).则两个正方形重叠部分的面积为$S_{\triangle BOF}+S_{\triangle BOE}=S_{\triangle AEO}+S_{\triangle BOE}=S_{\triangle ABO}$,即等于一个正方形面积的$\frac{1}{4}$.
∵四边形ABCD为正方形,
∴∠OAE=∠OBF=45°,BO⊥AC,即∠AOE+∠EOB=90°.又
∵四边形A'B'C'O为正方形,
∴∠A'OC'=90°,即∠BOE+∠BOC'=90°,
∴∠AOE=∠BOF.在△AOE和△BOF中,$\left\{\begin{array}{l}∠AOE=∠BOF,\\AO=BO,\\∠OAE=∠OBF,\end{array}\right.$
∴△AOE≌△BOF(ASA).则两个正方形重叠部分的面积为$S_{\triangle BOF}+S_{\triangle BOE}=S_{\triangle AEO}+S_{\triangle BOE}=S_{\triangle ABO}$,即等于一个正方形面积的$\frac{1}{4}$.
某校数学兴趣小组开展了一次课外活动,过程如下:如图①,在正方形 $ABCD$ 中,$AB = 4$,将三角尺放在正方形 $ABCD$ 上,使三角尺的直角顶点与点 $D$ 重合,三角尺的一边交 $AB$ 于点 $P$,另一边交 $BC$ 的延长线于点 $Q$。
(1)求证:$AP = CQ$;
(2)如图②,小明在图①的基础上作 $\angle PDQ$ 的平分线 $DE$ 交 $BC$ 于点 $E$,连接 $PE$,他发现 $PE$ 和 $QE$ 存在一定的数量关系,请猜测他的结论并予以证明;
(3)在(2)的条件下,若 $AP = 1$,求 $PE$ 的长。
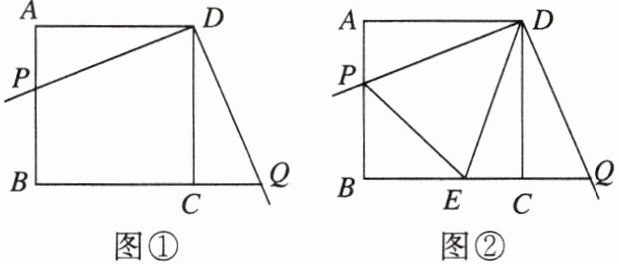
(1)求证:$AP = CQ$;
(2)如图②,小明在图①的基础上作 $\angle PDQ$ 的平分线 $DE$ 交 $BC$ 于点 $E$,连接 $PE$,他发现 $PE$ 和 $QE$ 存在一定的数量关系,请猜测他的结论并予以证明;
(3)在(2)的条件下,若 $AP = 1$,求 $PE$ 的长。

答案:
(1)证明:
∵四边形ABCD是正方形,
∴∠ADC=∠A=∠B=∠BCD=∠DCQ=90°,AD=BC=CD=AB=4.
∵∠PDQ=90°,
∴∠ADP=∠CDQ.在△APD和△CQD中,$\left\{\begin{array}{l}∠A=∠DCQ,\\AD=CD,\\∠ADP=∠CDQ,\end{array}\right.$
∴△APD≌△CQD(ASA),
∴AP=CQ.
(2)解:PE=QE.证明如下:由
(1)得△APD≌△CQD,
∴PD=QD.
∵DE平分∠PDQ,
∴∠PDE=∠QDE.在△PDE和△QDE中,$\left\{\begin{array}{l}PD=QD,\\∠PDE=∠QDE,\\DE=DE,\end{array}\right.$
∴△PDE≌△QDE(SAS),
∴PE=QE.
(3)解:由
(2)得PE=QE,由
(1)得CQ=AP=1,
∴BQ=BC+CQ=5,BP=AB - AP=3.设PE=QE=x,则BE=5 - x,在Rt△BPE中,由勾股定理得$3^{2}+(5 - x)^{2}=x^{2}$,解得x=3.4,即PE的长为3.4.
(1)证明:
∵四边形ABCD是正方形,
∴∠ADC=∠A=∠B=∠BCD=∠DCQ=90°,AD=BC=CD=AB=4.
∵∠PDQ=90°,
∴∠ADP=∠CDQ.在△APD和△CQD中,$\left\{\begin{array}{l}∠A=∠DCQ,\\AD=CD,\\∠ADP=∠CDQ,\end{array}\right.$
∴△APD≌△CQD(ASA),
∴AP=CQ.
(2)解:PE=QE.证明如下:由
(1)得△APD≌△CQD,
∴PD=QD.
∵DE平分∠PDQ,
∴∠PDE=∠QDE.在△PDE和△QDE中,$\left\{\begin{array}{l}PD=QD,\\∠PDE=∠QDE,\\DE=DE,\end{array}\right.$
∴△PDE≌△QDE(SAS),
∴PE=QE.
(3)解:由
(2)得PE=QE,由
(1)得CQ=AP=1,
∴BQ=BC+CQ=5,BP=AB - AP=3.设PE=QE=x,则BE=5 - x,在Rt△BPE中,由勾股定理得$3^{2}+(5 - x)^{2}=x^{2}$,解得x=3.4,即PE的长为3.4.
如图,在正方形 $ABCD$ 中,$E$ 是边 $AB$ 上的一动点(不与点 $A$,$B$ 重合),连接 $DE$,点 $A$ 关于直线 $DE$ 的对称点为 $F$,连接 $EF$ 并延长交 $BC$ 于点 $G$,连接 $DG$,过点 $E$ 作 $EH\perp DE$ 交 $DG$ 的延长线于点 $H$,连接 $BH$。
(1)求证:$GF = GC$;
(2)用等式表示线段 $BH$ 与 $AE$ 的数量关系,并证明。

(1)求证:$GF = GC$;
(2)用等式表示线段 $BH$ 与 $AE$ 的数量关系,并证明。

答案:
(1)证明:如图①,连接DF.
∵四边形ABCD是正方形,
∴DA=DC,∠A=∠C=90°.
∵点A关于直线DE的对称点为F,
∴△ADE≌△FDE,
∴DA=DF=DC,∠DFE=∠A=90°,
∴∠DFG=90°.在Rt△DFG和Rt△DCG中,$\left\{\begin{array}{l}DF=DC,\\DG=DG,\end{array}\right.$
∴Rt△DFG≌Rt△DCG(HL),
∴GF=GC.
(2)解:$BH=\sqrt{2}AE$.证明如下:证法一:如图②,连接DF,在线段AD上截取AM,使AM=AE.
∵AD=AB,
∴DM=BE.由
(1)知∠1=∠2,∠3=∠4,又
∵∠ADC=90°,
∴∠1+∠2+∠3+∠4=90°,
∴2∠2+2∠3=90°,
∴∠2+∠3=45°,即∠EDG=45°.
∵EH⊥DE,
∴∠DEH=90°,
∴△DEH是等腰直角三角形,
∴∠AED+∠BEH=∠AED+∠1=90°,DE=EH,
∴∠1=∠BEH,在△DME和△EBH中,$\left\{\begin{array}{l}DM=BE,\\∠1=∠BEH,\\DE=EH,\end{array}\right.$
∴△DME≌△EBH,
∴EM=BH.Rt△AEM中,∠A=90°,AM=AE,
∴$EM=\sqrt{2}AE$,
∴$BH=\sqrt{2}AE$. 证法二:如图③,连接DF,过点H作HN⊥AB于点N,
证法二:如图③,连接DF,过点H作HN⊥AB于点N,
∴∠BNH=90°.由证法一可知DE=EH,∠1=∠NEH.在△DAE和△ENH中,$\left\{\begin{array}{l}∠A=∠ENH,\\∠1=∠NEH,\\DE=EH,\end{array}\right.$
∴△DAE≌△ENH,
∴AE=HN,AD=EN.
∵AD=AB,
∴AB=EN=AE+BE=BE+BN,
∴AE=BN=HN,
∴△BNH是等腰直角三角形,
∴$BH=\sqrt{2}HN=\sqrt{2}AE$.
(1)证明:如图①,连接DF.
∵四边形ABCD是正方形,
∴DA=DC,∠A=∠C=90°.
∵点A关于直线DE的对称点为F,
∴△ADE≌△FDE,
∴DA=DF=DC,∠DFE=∠A=90°,
∴∠DFG=90°.在Rt△DFG和Rt△DCG中,$\left\{\begin{array}{l}DF=DC,\\DG=DG,\end{array}\right.$
∴Rt△DFG≌Rt△DCG(HL),
∴GF=GC.

(2)解:$BH=\sqrt{2}AE$.证明如下:证法一:如图②,连接DF,在线段AD上截取AM,使AM=AE.
∵AD=AB,
∴DM=BE.由
(1)知∠1=∠2,∠3=∠4,又
∵∠ADC=90°,
∴∠1+∠2+∠3+∠4=90°,
∴2∠2+2∠3=90°,
∴∠2+∠3=45°,即∠EDG=45°.
∵EH⊥DE,
∴∠DEH=90°,
∴△DEH是等腰直角三角形,
∴∠AED+∠BEH=∠AED+∠1=90°,DE=EH,
∴∠1=∠BEH,在△DME和△EBH中,$\left\{\begin{array}{l}DM=BE,\\∠1=∠BEH,\\DE=EH,\end{array}\right.$
∴△DME≌△EBH,
∴EM=BH.Rt△AEM中,∠A=90°,AM=AE,
∴$EM=\sqrt{2}AE$,
∴$BH=\sqrt{2}AE$.
 证法二:如图③,连接DF,过点H作HN⊥AB于点N,
证法二:如图③,连接DF,过点H作HN⊥AB于点N,∴∠BNH=90°.由证法一可知DE=EH,∠1=∠NEH.在△DAE和△ENH中,$\left\{\begin{array}{l}∠A=∠ENH,\\∠1=∠NEH,\\DE=EH,\end{array}\right.$
∴△DAE≌△ENH,
∴AE=HN,AD=EN.
∵AD=AB,
∴AB=EN=AE+BE=BE+BN,
∴AE=BN=HN,
∴△BNH是等腰直角三角形,
∴$BH=\sqrt{2}HN=\sqrt{2}AE$.

查看更多完整答案,请扫码查看


